强化学习的数学基础 - Chapter 1

赵老师开源的 Github 仓库、赵老师的 B站 课程视频

Overview

通过网格世界示例，我们展示了以下关键概念：

• 状态
• 动作
• 状态转移、状态转移概率 $p(s^\prime|s,a)$
• 奖励、奖励概率 $p(r|s,a)$
• 轨迹、回合、回报、折扣回报
• 马尔可夫决策过程

Lecture 1: State, Action, Policy

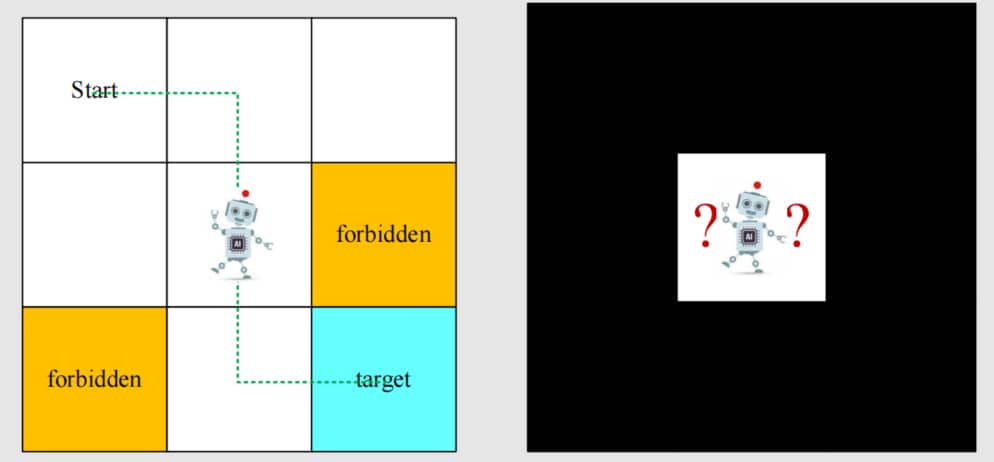Grid-World Example

课程中贯穿始终的案例：

• 单元格网格：accessible / forbidden / target cells / boundary
• 非常容易理解且对说明很有用

任务：

• 给定任何起始区域，找到一条通往目标的“好”路径。
• 如何定义“好”？尽可能避开禁止单元格、绕路或超越边界。

1.1 State

<span style="color:lightgreen">状态 (state) : agent 相对于环境的状态 (status)

• 对于 grid-world example，智能体的位置就是其状态。有九个可能的位置，因此有九个状态：$s_1, s_2, \dots, s_9$。

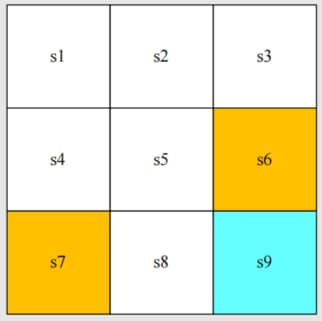State

<span style="color:lightgreen">状态空间 (state space) : 所有状态的集合 $\mathcal{S} = \{s_i\}_{i=1}^9$。

1.2 Action

<span style="color:lightgreen">动作 (action) : 对于每个状态，有五个可能的动作：$a_1, \dots, a_5$

• $a_1$：向上移动；
• $a_2$：向右移动；
• $a_3$：向下移动；
• $a_4$：向左移动；
• $a_5$：保持不变；

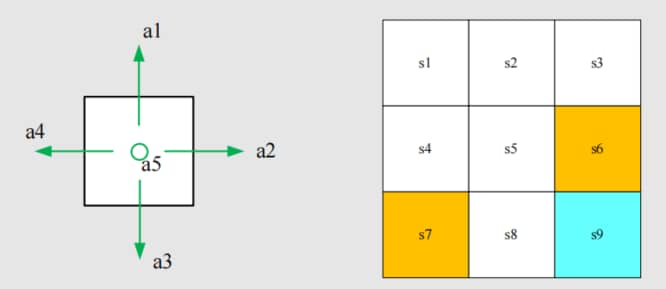State

<span style="color:lightgreen">动作空间 (action space of a state) : 一个状态的所有可能动作的集合。$\mathcal{A}(s_i) = \{a_i\}_{i=1}^5$。

Remark: 可以看到，动作空间是依赖于状态的。

1.3 State Transition

沿用上面的例子

当执行一个 action 时，agent 可能从一个状态转移到另一个状态。这样的过程称为 <span style="color:lightgreen">状态转移 (state transition)

• 在状态 $s_1$，如果我们选择动作 $a_2$，那么下一个状态是什么？

  $$s_1 \stackrel{a_2}{\longrightarrow} s_2$$

• 在状态 $s_1$，如果我们选择动作 $a_1$，那么下一个状态是什么？

  $$s_1 \stackrel{a_1}{\longrightarrow} s_1$$

• 状态转移定义了与环境的交互。

Q：我们可以用其他方式定义状态转移吗？可以。

1.3.1 Forbidden Area

Forbidden area: 在状态 $s_5$，如果我们选择动作 $a_2$，那么下一个状态是什么？

• 情况1：禁止区域可进入但有惩罚。此时，

  $$s_5 \stackrel{a_2}{\longrightarrow} s_6$$

• 情况2：禁止区域不可进入（例如，被墙包围）

  $$s_5 \stackrel{a_2}{\longrightarrow} s_5$$

我们考虑第一种情况，它更具一般性，也更困难。

1.3.2 Tabular Representation

我们可以用表格来描述状态转移：

	$a_1$ (upwards)	$a_2$ (rightwards)	$a_3$ (downwards)	$a_4$ (leftwards)	$a_5$ (unchanged)
$s_1$	$s_1$	$s_2$	$s_4$	$s_1$	$s_1$
$s_2$	$s_2$	$s_3$	$s_5$	$s_1$	$s_2$
$s_3$	$s_3$	$s_3$	$s_6$	$s_2$	$s_3$
$s_4$	$s_1$	$s_5$	$s_7$	$s_4$	$s_4$
$s_5$	$s_2$	$s_6$	$s_8$	$s_4$	$s_5$
$s_6$	$s_3$	$s_6$	$s_9$	$s_5$	$s_6$
$s_7$	$s_4$	$s_8$	$s_7$	$s_7$	$s_7$
$s_8$	$s_5$	$s_9$	$s_8$	$s_7$	$s_8$
$s_9$	$s_6$	$s_9$	$s_9$	$s_8$	$s_9$

但这仅能表示确定性情况。

1.3.3 State Transition Probability

<span style="color:lightgreen">状态转移概率 (state transition probability) : 用概率来描述状态转移！

• 直觉：在状态 $s_1$，如果我们选择动作 $a_2$，下一个状态是 $s_2$。
• 数学表达：

  $$\begin{align*} p(s_2|s_1,a_2)&=1 \\ p(s_i|s_1,a_2)&=0\quad \forall i \neq 2 \end{align*}$$

这是确定性情况。状态转移也可以是随机性的。

1.3 Policy

<span style="color:lightgreen">策略 (Policy) : 告诉 agent 在某个状态下采取什么动作。

直观表示：箭头展示了一个策略。

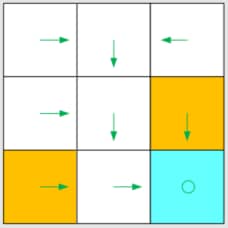Policy

基于这个策略，我们可以得到不同起始点的如下路径 (path)

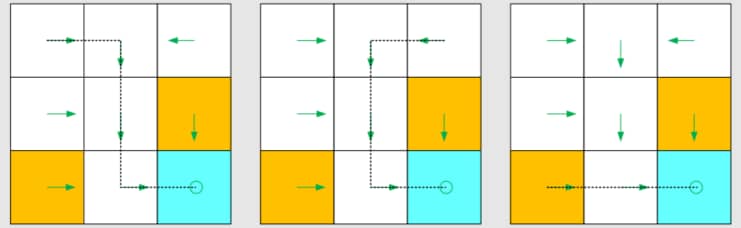Path / Trajectory

数学化的表达方式：使用条件概率。

例如，对于状态 $s_1$：

• $\pi(a_1|s_1)=0$
• $\pi(a_2|s_1)=1$
• $\pi(a_3|s_1)=0$
• $\pi(a_4|s_1)=0$
• $\pi(a_5|s_1)=0$

这是一个确定性策略。

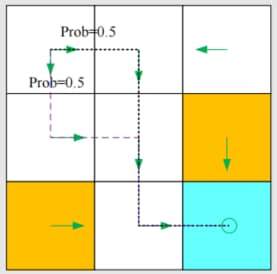不确定情况下的策略

在这个策略中，对于 $s_1$：

• $\pi(a_1|s_1)=0$
• $\pi(a_2|s_1)=0.5$
• $\pi(a_3|s_1)=0.5$
• $\pi(a_4|s_1)=0$
• $\pi(a_5|s_1)=0$

这是一个随机性策略。

策略的表格表示：

	$a_1$ (upwards)	$a_2$ (rightwards)	$a_3$ (downwards)	$a_4$ (leftwards)	$a_5$ (unchanged)
$s_1$	0	0.5	0.5	0	0
$s_2$	0	0	1	0	0
$s_3$	0	0	0	1	0
$s_4$	0	1	0	0	0
$s_5$	0	0	1	0	0
$s_6$	0	0	1	0	0
$s_7$	0	1	0	0	0
$s_8$	0	1	0	0	0
$s_9$	0	0	0	0	1

可表示确定性或随机性情况。

Lecture 2: Reward, Return, Markov Decision Process

2.1 Reward

<span style="color:lightgreen">奖励 (reward) : agent 在执行动作后获得的实数。

奖励是强化学习（RL）最独特的概念之一。

• 正奖励 (positive) 表示对采取此类动作的鼓励 (encourage)
• 负奖励 (negative) 表示对采取此类动作的惩罚 (punishment)

问题：

• 零奖励算是什么？无惩罚（一定程度上算是鼓励）
• 正奖励可以表示惩罚吗？可以。

2.1.1 网格世界示例中的奖励设计

在网格世界示例中，奖励设计如下：

• 如果智能体试图越界，令 $r_{\text{bound}} = -1$
• 如果智能体试图进入禁止单元格，令 $r_{\text{forbid}} = -1$
• 如果智能体到达目标单元格，令 $r_{\text{target}} = +1$
• 否则，智能体获得奖励 $r = 0$。

奖励可被理解为<span style="color:lightgreen">人机接口 (human-machine interface)，通过它我们可以引导智能体表现出我们期望的行为。

例如，通过上述设计的奖励，智能体将尝试避免越界或踏入禁止单元格。

	$a_1$ (upwards)	$a_2$ (rightwards)	$a_3$ (downwards)	$a_4$ (leftwards)	$a_5$ (unchanged)
$s_1$	$r_{\text{bound}}$	0	0	$r_{\text{bound}}$	0
$s_2$	$r_{\text{bound}}$	0	0	0	0
$s_3$	$r_{\text{bound}}$	$r_{\text{bound}}$	$r_{\text{forbid}}$	0	0
$s_4$	0	0	$r_{\text{forbid}}$	$r_{\text{bound}}$	0
$s_5$	0	$r_{\text{forbid}}$	0	0	0
$s_6$	0	$r_{\text{bound}}$	$r_{\text{target}}$	0	$r_{\text{forbid}}$
$s_7$	0	0	$r_{\text{bound}}$	$r_{\text{bound}}$	$r_{\text{forbid}}$
$s_8$	0	$r_{\text{target}}$	$r_{\text{bound}}$	$r_{\text{forbid}}$	0
$s_9$	$r_{\text{forbid}}$	$r_{\text{bound}}$	$r_{\text{bound}}$	0	$r_{\text{target}}$

（上述表格仅能表示确定性情况。）

2.1.2 数学描述：条件概率

• 直觉：在状态 $s_1$，如果我们选择动作 $a_1$，奖励是 -1。
• 数学表达：$p(r = -1|s_1,a_1) = 1$ 且 $p(r \neq -1|s_1,a_1) = 0$

Remark：

• 这里是确定性情况。奖励转移也可以是随机性的。
• 例如，如果你努力学习，你会获得奖励，但具体多少是不确定的。
• 奖励依赖于状态和动作，而非下一状态（例如，考虑 $s_1,a_1$ 和 $s_1,a_5$）。

2.2 Trajectory and Return

<span style="color:lightgreen">轨迹 (trajectory) 是 <span style="color:lightgreen">状态-动作-奖励链 (state-action-reward chain)：

$$s_1 \stackrel{a_2}{\underset{r=0}{\longrightarrow}} s_2 \stackrel{a_3}{\underset{r=0}{\longrightarrow}} s_5 \stackrel{a_3}{\underset{r=0}{\longrightarrow}} s_8 \stackrel{a_2}{\underset{r=1}{\longrightarrow}} s_9$$

该轨迹的 <span style="color:lightgreen">回报 (return) 是沿轨迹收集的所有奖励 (reward) 之和：

$$\text{return} = 0 + 0 + 0 + 1 = 1$$

Remark: return 是针对轨迹来定义的。

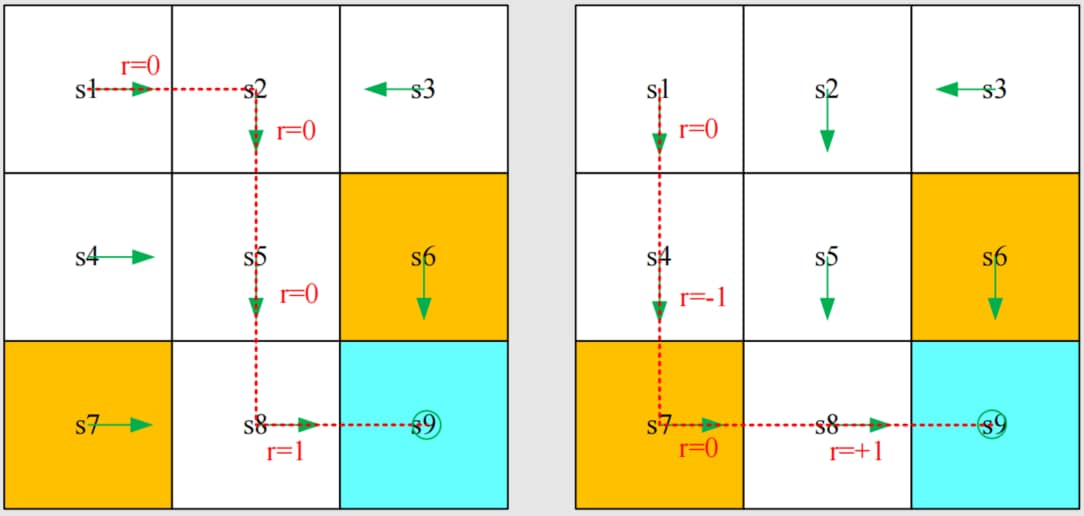不同 trajectory 的 return

不同的策略产生不同的轨迹

$$s_1 \stackrel{a_3}{\underset{r=0}{\longrightarrow}} s_4 \stackrel{a_3}{\underset{r=-1}{\longrightarrow}} s_7 \stackrel{a_2}{\underset{r=0}{\longrightarrow}} s_8 \stackrel{a_2}{\underset{r=+1}{\longrightarrow}} s_9$$

该路径的回报是：

$$\text{return} = 0 - 1 + 0 + 1 = 0$$

哪种策略更好？

• 直觉：第一种更好，因为它避开了禁止区域。
• 数学角度：第一种更好，因为它的 return 更大！
• return 可用于评估一个策略是否良好。

2.2.1 Discounted Return

轨迹可能是无限的：

$$s_1 \stackrel{a_2}{\longrightarrow} s_2 \stackrel{a_3}{\longrightarrow} s_5 \stackrel{a_3}{\longrightarrow} s_8 \stackrel{a_2}{\longrightarrow} s_9 \stackrel{a_5}{\longrightarrow} s_9 \stackrel{a_5}{\longrightarrow} s_9 \dots$$

回报为

$$\text{return} = 0 + 0 + 0 + 1 + 1 + 1 + \dots = \infty$$

由于回报发散，该定义无效！

如何解决？

需要引入 <span style="color:lightgreen">折扣因子 (discount rate) $\gamma \in [0,1)$

折扣回报 (Discounted Return)：

$$\begin{aligned} \text{discounted return} &= 0 + \gamma 0 + \gamma^2 0 + \gamma^3 1 + \gamma^4 1 + \gamma^5 1 + \dots \\ &= \gamma^3(1 + \gamma + \gamma^2 + \dots) = \gamma^3 \frac{1}{1 - \gamma}. \end{aligned}$$

作用：

• 求和变为有限；
• 平衡远期和近期未来的奖励：
  • 若 $\gamma$ 接近 0，折扣回报的值由近期获得的奖励主导。
  • 若 $\gamma$ 接近 1，折扣回报的值由远期获得的奖励主导。

2.3 Episode

遵循策略与环境交互时，智能体可能在某些终止状态 (terminal state) 停止，由此产生的轨迹称为 <span style="color:lightgreen">回合 (episode) 或 <span style="color:lightgreen">试验 (trial)。

$$s_1 \stackrel{a_2}{\underset{r=0}{\longrightarrow}} s_2 \stackrel{a_3}{\underset{r=0}{\longrightarrow}} s_5 \stackrel{a_3}{\underset{r=0}{\longrightarrow}} s_8 \stackrel{a_2}{\underset{r=1}{\longrightarrow}} s_9$$

episode 通常被假设为有限轨迹，这种任务通常称为 <span style="color:lightgreen">回合制任务 (episodic tasks)。

有些任务可能没有终止状态，这意味着与环境的交互永远不会结束。此类任务称为 <span style="color:lightgreen">持续性任务 (continuing tasks)。

在网格世界示例中，到达目标后我们应该停止吗？
实际上，我们可以通过将幕式任务转换为持续任务，以统一的数学方式处理回合制任务和持续性任务。

• 选择1：将目标状态视为特殊的 <span style="color:lightgreen">吸收态 (absorbing state)。一旦智能体到达吸收状态，就永远不会离开，后续奖励 $r = 0$。
• 选项2：将目标状态视为具有策略的正常状态。智能体仍可离开目标状态，且进入目标状态时获得 $r = +1$。

本课程中我们考虑选项2，这样我们就不需要将目标状态与其他状态区分开，可以将其视为正常状态。

2.4 Markov Decision Process (MDP)

• 集合：
  • 状态：状态集合 $\mathcal{S}$
  • 动作：与状态 $s \in \mathcal{S}$ 相关联的动作集合 $\mathcal{A}(s)$
  • 奖励：奖励集合 $\mathcal{R}(s,a)$
• 概率分布：
  • 状态转移概率：在状态 $s$，采取动作 $a$，转移到状态 $s^\prime$ 的概率是 $p(s^\prime|s,a)$
  • 奖励概率：在状态 $s$，采取动作 $a$，获得奖励 $r$ 的概率是 $p(r|s,a)$
• 策略：在状态 $s$，选择动作 $a$ 的概率是 $\pi(a|s)$
• 马尔可夫性：无记忆性

  $$\begin{align*} p(s_{t+1}|a_t, s_t, \dots, a_0, s_0) &= p(s_{t+1}|a_t, s_t), \\ p(r_{t+1}|a_t, s_t, \dots, a_0, s_0) &= p(r_{t+1}|a_t, s_t). \end{align*}$$

本讲介绍的所有概念都可以纳入 MDP 的框架中。

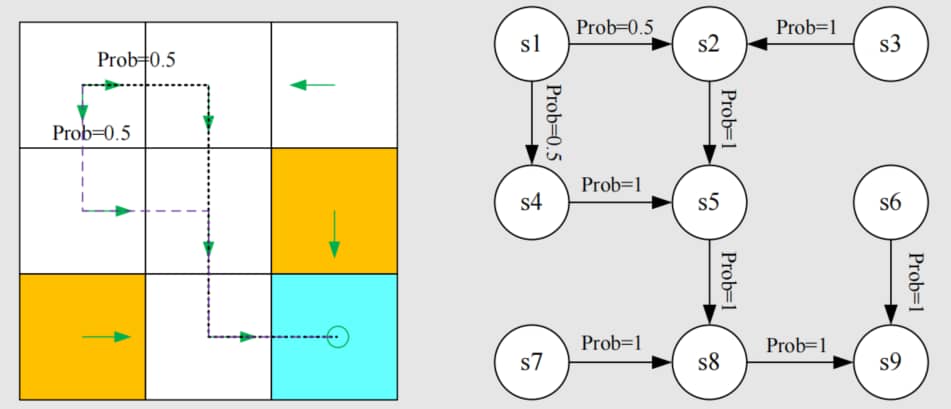从 MDP 框架下再看网格世界例子

• 圆圈代表状态，带箭头的连线代表状态转移。
• 给定策略后，马尔可夫决策过程就成为马尔可夫过程！