本文最后更新于 2025年10月26日 上午
10.20 - 10.23 0:30
以下内容均来自于 CS336 课堂教学与课后讲稿,仅供学习参考。如有错误,请在下方评论区指出,谢谢!
Lec01:overview, tokenization
0. Motivating Questions
本讲概述:
讨论训练模型所需的所有 基本组件 (primitives)
从张量 (tensors) 到模型,再到优化器,最后到训练循环,自底向上地 (bottom-up) 讲解。
密切关注效率(资源 (resources) 的使用)
具体来说,我们将考虑两种类型的资源:
内存 (memory) GB
计算量 (compute) FLOPS
napkin math: 指对系统相关性能、资源消耗的快速估算
Q1: 在 15T 个 tokens 上,训练一个 70B 参数的模型,如果 1024 块 H100 显卡训练,需要多长时间?
1 2 3 4 5 total_flops = 6 * 70e9 * 15e12 = 6.300e+24 1979e12 / 2 0.5 1024 * 60 * 60 * 24 = 4.377e+22 143.927
Q2: 使用 AdamW 的情况下(naively),8 块 H100 显卡能训练的最大模型有多大?
1 2 3 h100_bytes = 80e9 4 + 4 + (4 + 4 ) = 16 8 ) / bytes_per_parameter = 4.000e+10 = 40 B
警告 (Caveat);上面是一个非常粗糙的计算,因为未考虑激活值(取决于 batch size 和 sequence length)。
我们将使用简单模型讲解,需要掌握的知识:
机制 (Mechanics):简单直接(仅用 PyTorch)
思维方式 (Mindset):资源核算(记得去做)
直觉 (Intuitions):大致框架(不涉及大模型)
1. Memory accounting
Pytorch docs on tensors
1.1 tensors basics
张量 (tensors) 是存储所有内容的基本构建块:参数、梯度、优化器状态、数据、激活值。
你可以通过多种方式创建张量:
1 2 3 4 x = torch.tensor([[1. , 2 , 3 ], [4 , 5 , 6 ]])4 , 8 ) 4 , 8 ) 4 , 8 )
分配 (allocate) 内存但不初始化 (initialize) 值:
如果需要,可以对参数使用一些自定义逻辑进行初始化
1 nn.init.trunc_normal_(x, mean=0 , std=1 , a=-2 , b=2 )
1.2 tensors memory
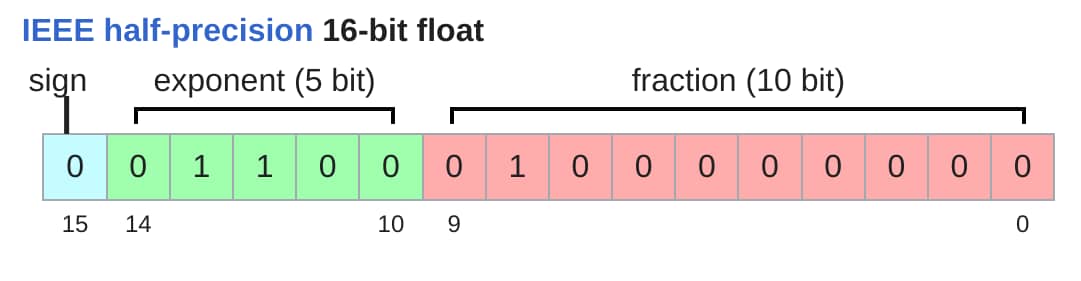
1.2.1 float32
float32 Wikipedia
fp32 单精度 示意图
float32 数据类型(也称为 fp32 或单精度 (single precision))是默认类型。
传统上,在科学计算中,float32 是基准;在某些情况下,你可以使用双精度(float64)。
在深度学习中,float32 通常已经足够精确了。
内存由(i)值的数量和(ii)每个值的数据类型决定。
1 2 3 4 5 x = torch.zeros(4 , 8 )assert x.dtype == torch.float32 assert x.numel() == 4 * 8 assert x.element_size() == 4 assert get_memory_usage(x) == 4 * 8 * 4
GPT-3前馈层中的一个矩阵:
1 assert get_memory_usage(torch.empty(12288 * 4 , 12288 )) == 2304 * 1024 * 1024
1.2.2 float16
float16 Wikipedia
fp16 半精度 示意图
float16数据类型(也称为 fp16 或 半精度 (half precision))可减少内存占用。
1 2 x = torch.zeros(4 , 8 , dtype=torch.float16)2
然而,其动态范围(尤其是对小数的表示)并不理想。
1 2 x = torch.tensor([[1e-8 ]], dtype=torch.float16)0
如果在训练时出现这种情况,可能会导致不稳定性。
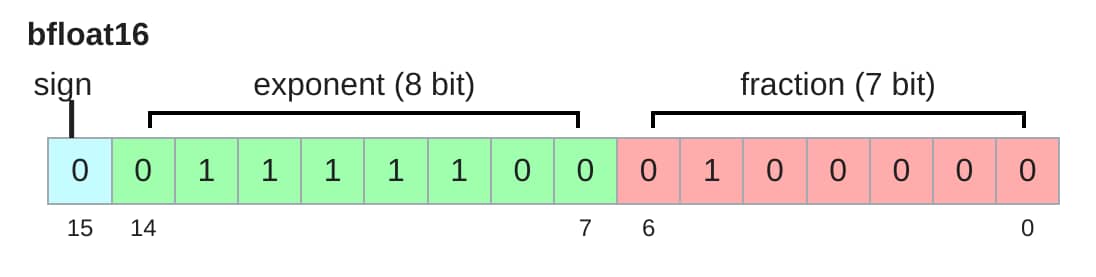
1.2.3 bfloat16
bfloat16 Wikipedia
bfloat = Brain Floating Point
Google Brain 于 2018 年开发了 bfloat 来解决数据表示的 动态范围问题 ,而不是小数部分的精度。
bfloat16 与 float16 占用相同的内存,但具有与float32 相同的动态范围!唯一的不足是分辨率更差,但这在深度学习中不那么重要。
1 2 x = torch.tensor([[1e-8 ]], dtype=torch.bfloat16)1.0011717677116394e-8
比较不同数据类型的动态范围和内存使用情况:
1 2 3 float32_info = torch.finfo(torch.float32)
得到
1 2 3 float32_info ="finfo(resolution=1e-06, min=-3.40282e+38, max=3.40282e+38, eps=1.19209e-07, smallest_normal=1.17549e-38, tiny=1.17549e-38, dtype=float32)" "finfo(resolution=0.001, min=-65504, max=65504,eps=0.000976562, smallest_normal=6.10352e-05, tiny=6.10352e-05, dtype=float16)" "finfo(resolution=0.01, min=-3.38953e+38, max=3.38953e+38, eps=0.0078125, smallest_normal=1.17549e-38, tiny=1.17549e-38, dtype=bfloat16)"
1.2.4 float8
float8 Nvidia
2022年,受机器学习工作负载推动,FP8 格式被正式确立为标准。
float8 示意图
H100 显卡支持两种 FP8 变体:[[Micikevicius+ 2022]]
E4M3: [-448, 448]
E5M2: [-57344, 57344]
1.2.5 Summary
精度选择对训练的影响:
使用 float32 训练可行,但需要大量内存。
使用 fp8、float16 甚至 bfloat16 训练存在风险,可能会出现不稳定性。
解决方案(后续讲解):仔细查看 pipeline,弄清楚在前向传播、反向传播、优化器、梯度累积等特定环节具体需要多低的精度,进而使用 混合精度训练 (参见mixed precision training)
精度的常见选择:
注意力机制:FP32
简单前向传播:BF16
需要长时间累积的环节,可能会更倾向于使用 FP32
2. Compute accounting
2.1 tensors on gpus
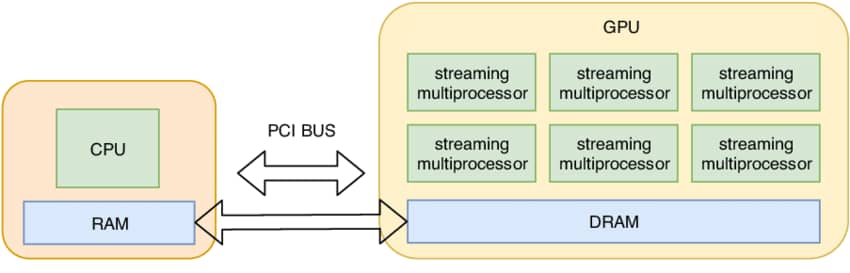
默认情况下,张量存储在 CPU 内存中。
1 2 x = torch.zeros(32 , 32 )assert x.device == torch.device("cpu" )
然而,为了利用 GPU 的大规模并行性,我们需要将它们移到 GPU 内存中。
将数据在 CPU 与 GPU 之间传输
让我们先看看是否有 GPU。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 if not torch.cuda.is_available():return for i in range (num_gpus):"cuda:0" ) assert y.device == torch.device("cuda" , 0 )32 , 32 , device="cuda:0" )assert memory_used == 2 * (32 * 32 * 4 )
以上就是一个用于检查代码是否正常工作的完整性检查 (sanity check)
2.2 tensor operations
大多数张量是通过对其他张量执行操作来创建的。每个操作都会带来一定的内存和计算开销。
2.2.1 tensor storage
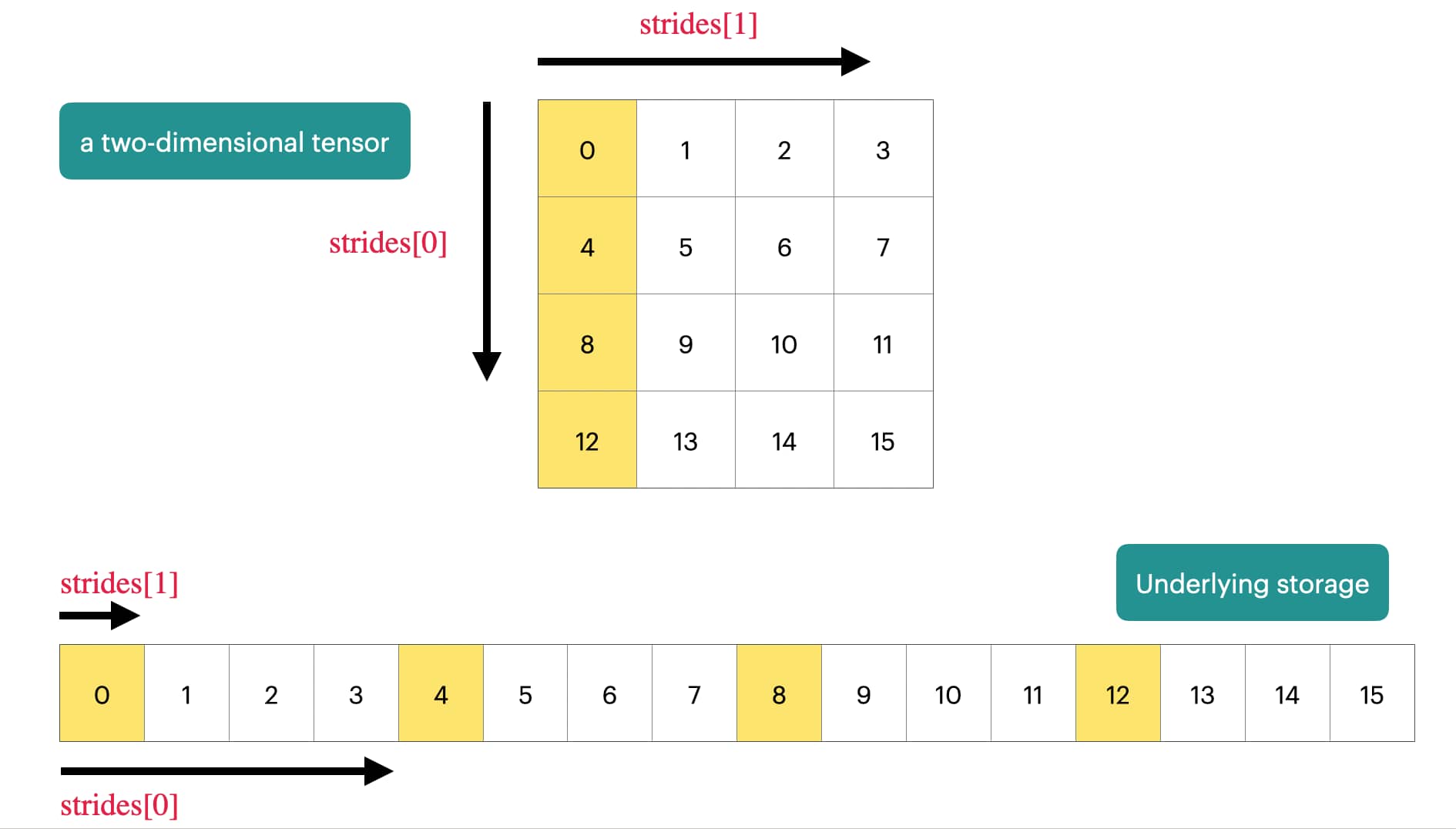
PyTorch 中的张量是什么?
PyTorch 张量是指向已分配内存的指针
张量带有描述如何获取张量中任意元素的元数据。
二维情形的张量示意图
Tensor Stride - PyTorch 文档
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 x = torch.tensor([0. , 1 , 2 , 3 ],4 , 5 , 6 , 7 ],8 , 9 , 10 , 11 ],12 , 13 , 14 , 15 ],assert x.stride(0 ) == 4 assert x.stride(1 ) == 1 1 , 2 0 ) + c * x.stride(1 )assert index == 6
2.2.2 tensor slicing
这一点允许我们让多个张量共享同一块存储空间,不用到处复制张量
许多操作只是提供了张量的不同 视图 (view)
这不会创建副本,因此对一个张量的修改可能会影响另一个张量。
下面的 x 与 y 共享同一块存储空间
1 2 3 4 5 6 7 x = torch.tensor([[1. , 2 , 3 ], [4 , 5 , 6 ]])0 ] 1 ]
将 2x3 矩阵视为 3x2 矩阵:
转置:
修改 x 也会修改 y
1 2 x[0 ][0 ] = 100 assert y[0 ][0 ] == 100
注意,有些 view 对张量的访问是不连续的,这意味着无法再创建进一步的视图。
1 2 3 4 5 6 7 8 x = torch.tensor([[1. , 2 , 3 ], [4 , 5 , 6 ]])1 , 0 ) assert not y.is_contiguous()try :2 , 3 )assert False except RuntimeError as e:assert "view size is not compatible with input tensor's size and stride" in str (e)
可以先强制将张量变为连续的:使用 contiguous() 或者 reshape() 函数:
1 2 y = x.transpose(1 , 0 ).contiguous().view(2 , 3 )assert not same_storage(x, y)
张量视图是不占空间的 (free),复制则会占用(额外的)内存和计算资源。
2.2.3 tensor elementwise
这些操作对张量的每个元素应用某种运算并返回一个(新的)形状相同的张量。
1 2 3 4 5 6 7 8 x = torch.tensor([1 , 4 , 9 ])assert torch.equal(x.pow (2 ), torch.tensor([1 , 16 , 81 ]))assert torch.equal(x.sqrt(), torch.tensor([1 , 2 , 3 ]))assert torch.equal(x.rsqrt(), torch.tensor([1 , 1 /2 , 1 /3 ])) assert torch.equal(x + x, torch.tensor([2 , 8 , 18 ]))assert torch.equal(x * 2 , torch.tensor([2 , 8 , 18 ]))assert torch.equal(x / 0.5 , torch.tensor([2 , 8 , 18 ]))
triu 提取矩阵的上三角部分。
1 2 3 4 5 6 x = torch.ones(3 , 3 ).triu() assert torch.equal(x, torch.tensor([1 , 1 , 1 ],0 , 1 , 1 ],0 , 0 , 1 ],
这对于计算因果注意力掩码很有用,其中 M[i,j] 是 i 对 j 的贡献。
2.2.4 tensor matmul
最后介绍以下深度学习的核心:矩阵乘法。
1 2 3 4 x = torch.ones(16 , 32 )32 , 2 )assert y.size() == torch.Size([16 , 2 ])
操作轮次
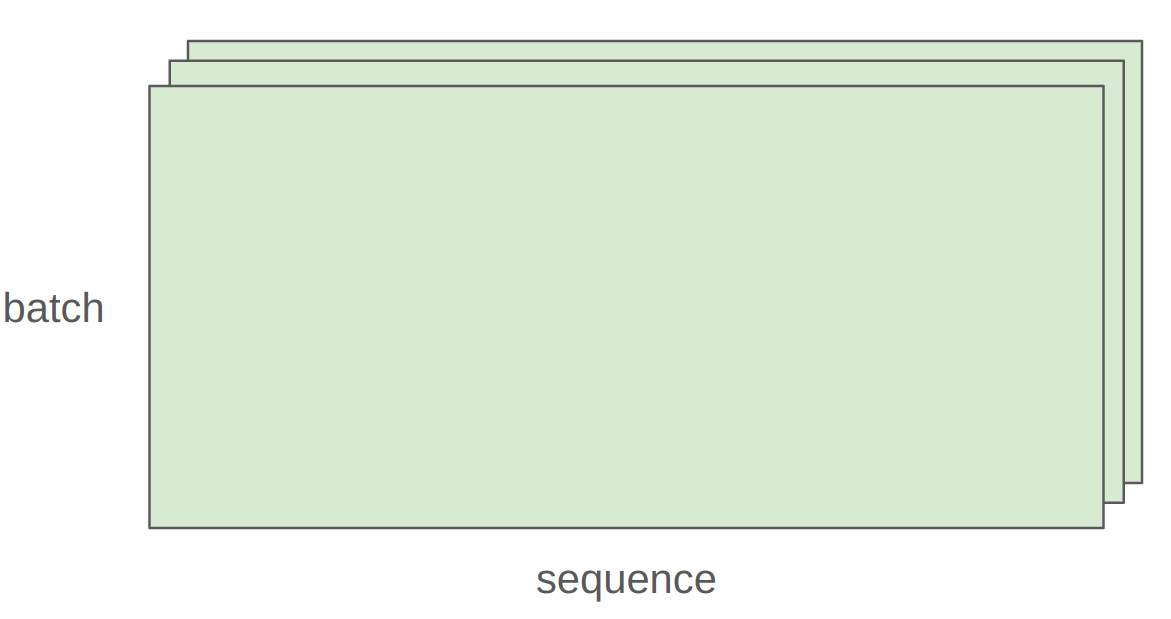
一般来说,我们会对 batch 中的每个 example 以及 sequence 中的每个 token 执行操作。
1 2 3 4 x = torch.ones(4 , 8 , 16 , 32 )32 , 2 )assert y.size() == torch.Size([4 , 8 , 16 , 2 ])
在这种情况下,我们遍历 x 的前 2 个维度的值,后 2 个维度与 w 相乘。
2.3 tensor einops
2.3.0 einops motivation
Einops tutorial
Einops 是一个用于操作 维度具名 张量的库。它的灵感来自爱因斯坦求和符号 [Einstein, 1916]。
传统 PyTorch 代码:
1 2 3 x = torch.ones(2 , 2 , 3 ) 2 , 2 , 3 ) 2 , -1 )
此类反向索引,很容易搞混维度(什么是 -2、-1?)
2.3.1 jaxtyping basics
如何跟踪张量的维度?
旧方法:
1 x = torch.ones(2 , 2 , 1 , 3 )
新方法: jaxtyping
1 x: Float[torch.Tensor, "batch seq heads hidden" ] = torch.ones(2 , 2 , 1 , 3 )
Note: 此处只是文档说明(无强制约束)。
2.3.2 einops einsum
Einsum 是带有良好维度记录的广义矩阵乘法。
定义两个张量:
1 2 x: Float[torch.Tensor, "batch seq1 hidden" ] = torch.ones(2 , 3 , 4 )"batch seq2 hidden" ] = torch.ones(2 , 3 , 4 )
旧方法:
1 z = x @ y.transpose(-2 , -1 )
新方法: einops
1 z = einsum(x, y, "batch seq1 hidden, batch seq2 hidden -> batch seq1 seq2" )
输出中未命名的维度会被求和(比如 hidden),输出中任何被命名的维度都会被遍历。
或者可以使用 ... 表示对任意数量的维度进行广播:
1 z = einsum(x, y, "... seq1 hidden, ... seq2 hidden -> ... seq1 seq2" )
2.3.3 einops reduce
你可以通过某些操作(例如,sum, mean, max, min)对单个张量进行约简。
1 x: Float[torch.Tensor, "batch seq hidden" ] = torch.ones(2 , 3 , 4 )
旧方法:对最后一个维度求和
新方法: einops
1 y = reduce(x, "... hidden -> ..." , "sum" )
2.3.4 einops rearrange
有时,一个维度代表两个维度,而你想对其中一个维度进行操作。
1 x: Float[torch.Tensor, "batch seq total_hidden" ] = torch.ones(2 , 3 , 8 )
其中 total_hidden 是 heads * hidden1 的扁平化表示
1 w: Float[torch.Tensor, "hidden1 hidden2" ] = torch.ones(4 , 4 )
将 total_hidden 拆分为两个维度(heads 和 hidden1):
1 x = rearrange(x, "... (heads hidden1) -> ... heads hidden1" , heads=2 )
通过 w 执行变换:
1 x = einsum(x, w, "... hidden1, hidden1 hidden2 -> ... hidden2" )
将 heads 和 hidden2 重新组合:
1 x = rearrange(x, "... heads hidden2 -> ... (heads hidden2)" )
2.4 tensor operations flops
在了解了所有操作之后,让我们来检查它们的计算成本。
浮点运算(FLOP)是像加法(x + y)或乘法(x * y)这样的基本运算。
两个极易混淆的首字母缩写词(发音相同!):
FLOPs:浮点运算次数(用于衡量完成的计算量)
FLOP/s:每秒浮点运算次数(也写作 FLOPS),用于衡量硬件的速度。
2.4.1 Intuitions
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 训练 GPT-3 (2020) 耗费了 3.14e23 次浮点运算。[[article ]](https://lambdalabs.com/blog/demystifying-gpt-3)[article ]](https://patmcguinness.substack.com/p/gpt-4-details-revealed)> teraFLOP/s = 万亿次浮点运算/s = 1e12 次 FLOP/s [spec ]](https://www.nvidia.com/content/dam/en-zz/Solutions/Data-Center/a100/pdf/nvidia-a100-datasheet-us-nvidia-1758950-r4-web.pdf)[spec ]](https://resources.nvidia.com/en-us-tensor-core/nvidia-tensor-core-gpu-datasheet)```python total_flops = 8 * (60 * 60 * 24 * 7) * h100_flop_per_sec == 4.788e+21
2.4.2 Linear Model
作为动机,假设你有一个线性模型。
有 n 个点
每个点是 d 维的
该线性模型将每个 d 维向量映射到 k 个输出
1 2 3 4 5 6 7 8 9 10 11 12 13 if torch.cuda.is_available():16384 32768 8192 else :1024 256 64
上述过程中的计算量:
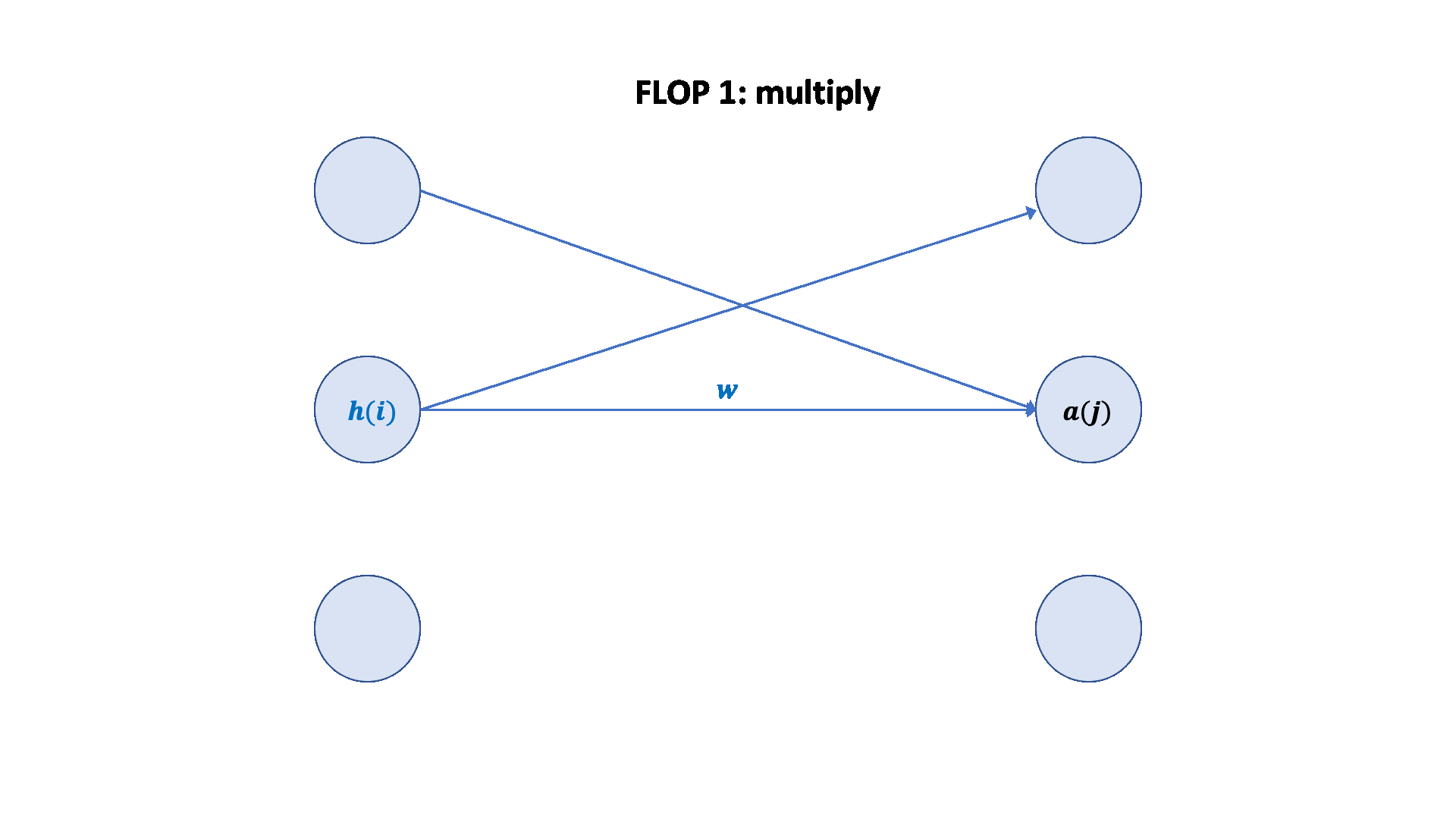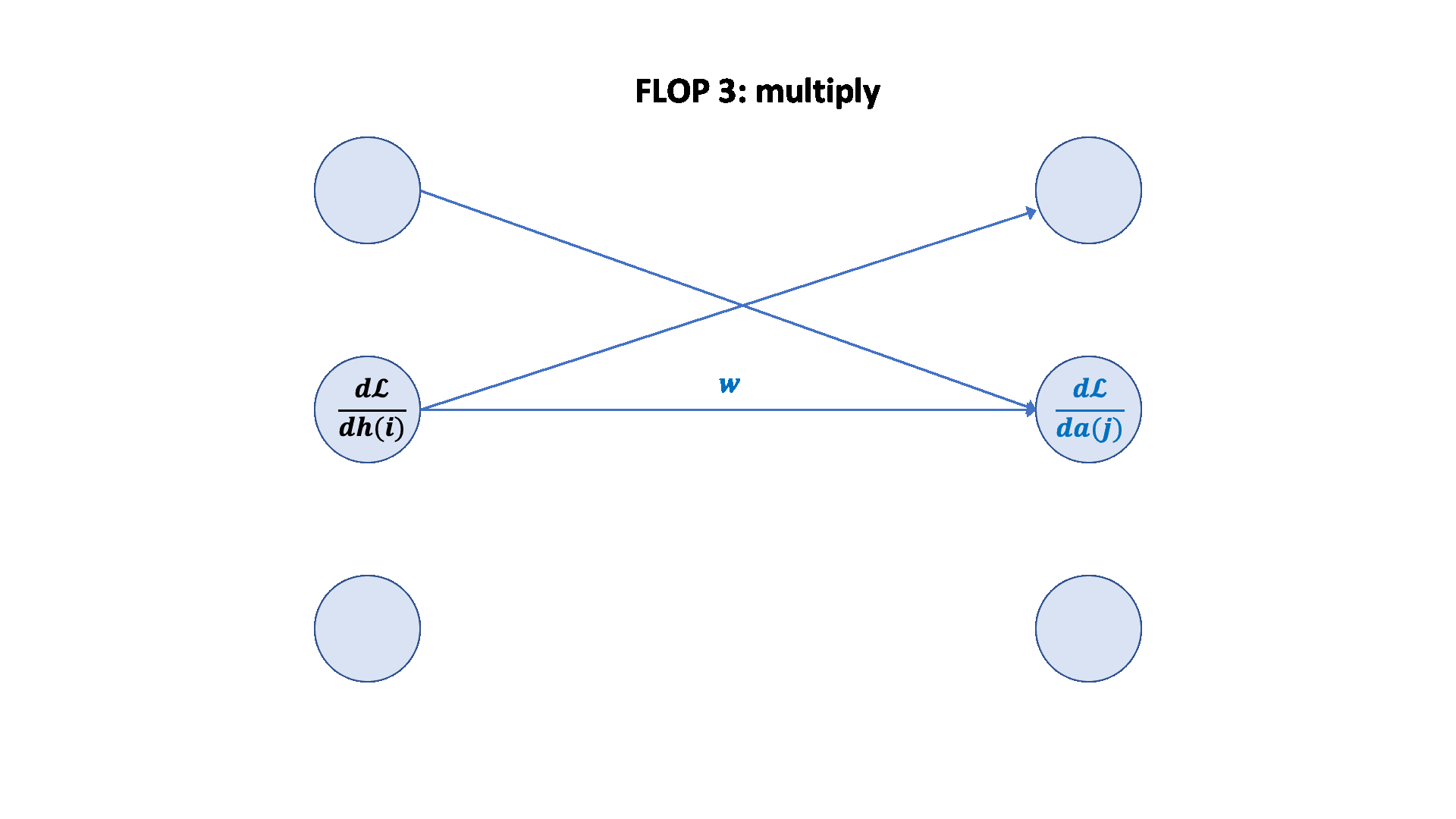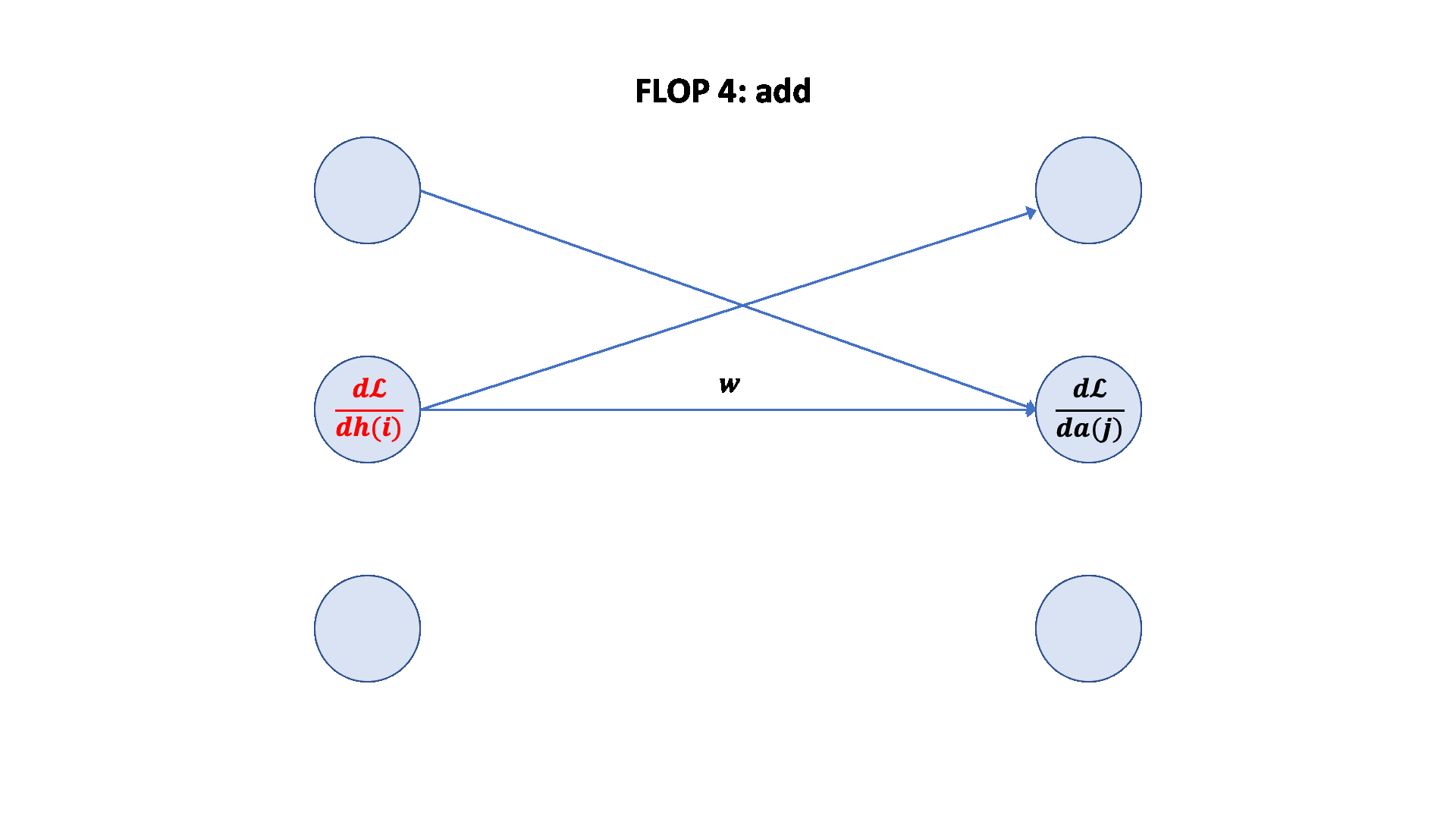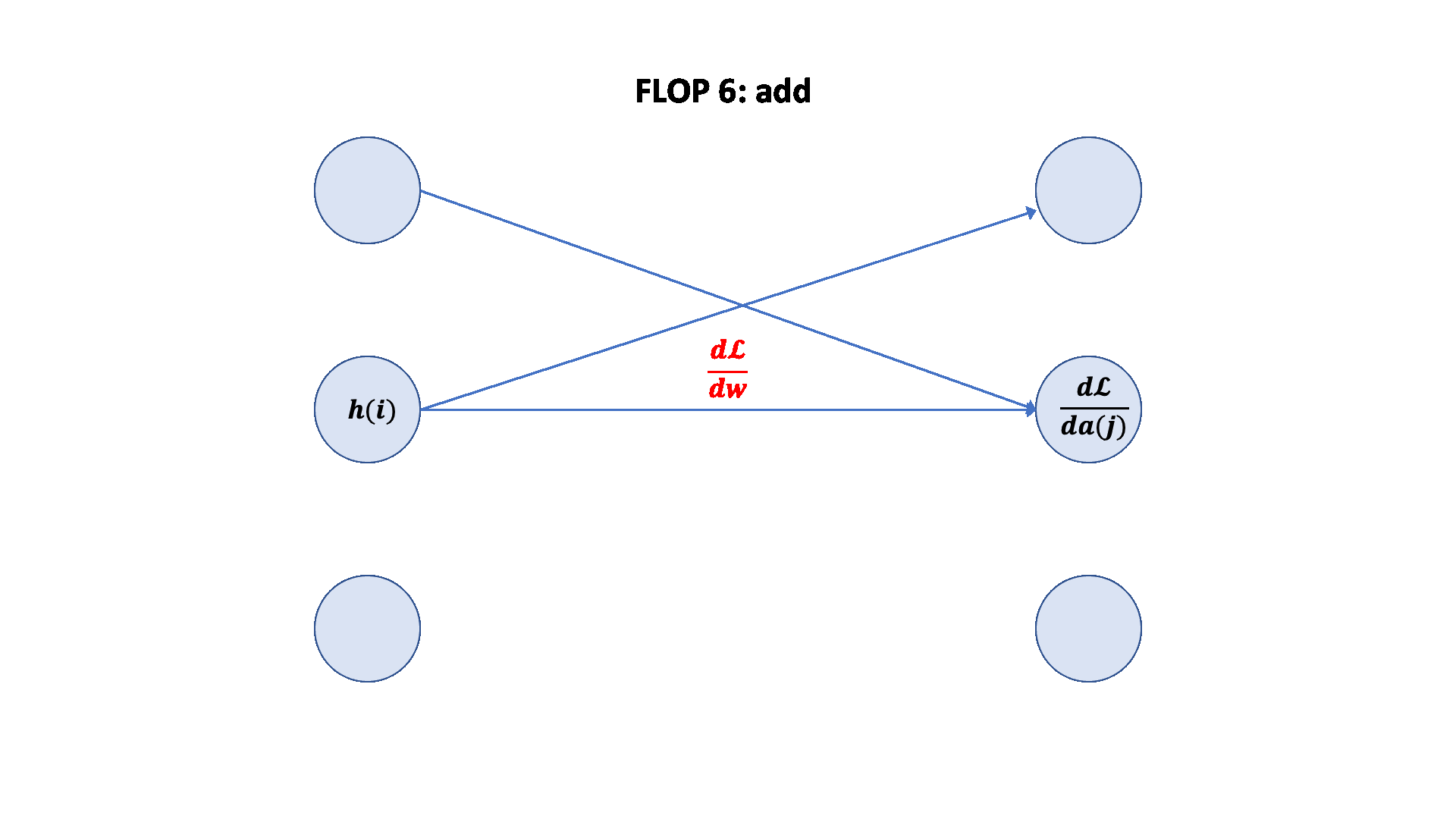
我们对每个 ( i , j , k ) (i, j, k) ( i , j , k ) x [ i ] [ j ] ∗ w [ j ] [ k ] x[i][j] * w[j][k] x [ i ] [ j ] ∗ w [ j ] [ k ]
1 2 actual_num_flops = 2 * B * D * K8.796e+12
2.4.3 FLOPs of other operations
对一个 m × n m \times n m × n O ( m n ) O(m n) O ( mn )
两个 m × n m \times n m × n m n m n mn
一般来说,对于足够大的矩阵,在深度学习中你遇到的其他任何运算都不会像矩阵乘法那样昂贵。
解释:
B 是数据点的数量
(D K) 是参数的数量
前向传播的 FLOPs 是 2 ×(# token)×(# parameter)
事实证明,这可以推广到 Transformer。
我们的 FLOPs 如何转换为实际耗时(s) ?让我们来计时!
1 2 3 4 5 actual_time = time_matmul(x, w) 0.163 5.407e+13
每个 GPU 都有一份报告峰值性能的规格表。
请注意,FLOP/s 在很大程度上取决于 数据类型 !
1 2 promised_flop_per_sec = get_promised_flop_per_sec(device, x.dtype)6.750e+13
2.4.4 Model FLOPs utilization (MFU)
MFU 定义:(实际浮点运算/秒)/(标称浮点运算/秒) [忽略通信/开销]
1 2 mfu = actual_flop_per_sec / promised_flop_per_sec0.801
通常,MFU >= 0.5 就相当不错了(如果矩阵乘法占主导,这个值会更高)
让我们用 bfloat16 来做:
1 2 3 4 5 6 7 8 9 10 11 12 13 x = x.to(torch.bfloat16)0.032 2.735e+14 9.895e+14 0.276
Note:与 float32 相比,bfloat16 的实际浮点运算/秒更高。
这里的 MFU 相当低,可能是因为标称浮点运算次数有点乐观。
2.4.5 Summary
矩阵乘法占主导:(2 m n p) FLOPs
FLOP/s 取决于 <span style="color: lightgreen;">硬件(H100 >> A100)和 <span style="color: lightgreen;">数据类型(bfloat16 >> float32)
模型浮点运算利用率(MFU):(实际浮点运算/秒)/(标称浮点运算/秒)
2.5 gradients basics
到目前为止,我们已经构造了张量(对应于参数或数据),并通过运算(前向)传递它们。
现在,我们将计算梯度(反向)。
作为一个简单的例子,让我们考虑这个简单的线性模型:y = 0.5 ( x ∗ w − 5 ) 2 y = 0.5 (x * w - 5)^2 y = 0.5 ( x ∗ w − 5 ) 2
前向传播:计算损失
1 2 3 4 x = torch.tensor([1. , 2 , 3 ])1. , 1 , 1 ], requires_grad=True ) 0.5 * (pred_y - 5 ).pow (2 )
反向传播:计算梯度
1 2 3 4 5 6 loss.backward()assert loss.grad is None assert pred_y.grad is None assert x.grad is None assert torch.equal(w.grad, torch.tensor([1. , 2 , 3 ]))
2.6 gradients flops
接下来计算以下求梯度过程中的 FLOPs
重新审视我们的线性模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 if torch.cuda.is_available():16384 32768 8192 else :1024 256 64 True )True )
Model:x --w1–> h1 --w2–> h2 -> loss
1 2 3 h1 = x @ w1pow (2 ).mean()
回顾前向传播的浮点运算次数:tensor_operations_flops
乘法 x [ i ] [ j ] ∗ w 1 [ j ] [ k ] x[i][j] * w1[j][k] x [ i ] [ j ] ∗ w 1 [ j ] [ k ]
加法 h 1 [ i ] [ k ] h1[i][k] h 1 [ i ] [ k ]
乘法 h 1 [ i ] [ j ] ∗ w 2 [ j ] [ k ] h1[i][j] * w2[j][k] h 1 [ i ] [ j ] ∗ w 2 [ j ] [ k ]
加法 h 2 [ i ] [ k ] h2[i][k] h 2 [ i ] [ k ]
1 num_forward_flops = (2 * B * D * D) + (2 * B * D * K)
反向传播的浮点运算次数是多少?
1 2 3 h1.retain_grad()
回顾 Model:x --w1–> h1 --w2–> h2 -> loss
h1.grad = d loss / d h1
h2.grad = d loss / d h2
w1.grad = d loss / d w1
w2.grad = d loss / d w2
聚焦参数 w2,应用链式法则。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 num_backward_flops = 0 assert w2.grad.size() == torch.Size([D, K])assert h1.size() == torch.Size([B, D])assert h2.grad.size() == torch.Size([B, K])2 * B * D * Kassert h1.grad.size() == torch.Size([B, D])assert w2.size() == torch.Size([D, K])assert h2.grad.size() == torch.Size([B, K])2 * B * D * K 2 + 2 ) * B * D * D
动画来源的 blog
一个不错的图形化可视化(记得关闭深色模式,否则会是黑色背景)
总结:
前向传播:2 × ( # data points ) × ( # parameters ) 2 \times (\# \ \text{data points}) \times (\# \ \text{parameters}) 2 × ( # data points ) × ( # parameters )
反向传播:4 × ( # data points ) × ( # parameters ) 4 \times (\# \ \text{data points}) \times (\# \ \text{parameters}) 4 × ( # data points ) × ( # parameters )
总计:6 × ( # data points ) × ( # parameters ) 6 \times (\# \ \text{data points}) \times (\# \ \text{parameters}) 6 × ( # data points ) × ( # parameters )
3. Models
3.1 module parameters
1 2 input_dim = 16384 32
模型参数在 PyTorch 中以 nn.Parameter 对象的形式存储。
1 2 3 w = nn.Parameter(torch.randn(input_dim, output_dim))assert isinstance (w, torch.Tensor) assert type (w.data) == torch.Tensor
3.1.1 参数初始化
让我们看看会发生什么。
1 2 3 x = nn.Parameter(torch.randn(input_dim))assert output.size() == torch.Size([output_dim])
注意,output 的每个元素的规模为 sqrt(input_dim):53.789207458496094
较大的值会导致梯度爆炸,使训练不稳定。
我们希望初始化方式与 input_dim 无关。1/sqrt(input_dim) 重新缩放
1 2 w = nn.Parameter(torch.randn(input_dim, output_dim) / np.sqrt(input_dim))
现在 output 的每个元素都是常数:-1.0617939233779907
在常数范围内,这就是 Xavier 初始化。[论文] [stackexchange]
为了更安全,我们将正态分布截断到 [ − 3 , 3 ] [-3, 3] [ − 3 , 3 ]
1 w = nn.Parameter(nn.init.trunc_normal_(torch.empty(input_dim, output_dim), std=1 / np.sqrt(input_dim), a=-3 , b=3 ))
3.2 custom model
我们使用 nn.Parameter 构建一个简单的深度线性模型。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 D = 64 2 for name, param in model.state_dict().items()assert param_sizes == ["layers.0.weight" , D * D),"layers.1.weight" , D * D),"final.weight" , D),assert num_parameters == (D * D) + (D * D) + D
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Linear (nn.Module):"""简单的线性层。""" def __init__ (self, input_dim: int , output_dim: int ):super ().__init__()self .weight = nn.Parameter(torch.randn(input_dim, output_dim) / np.sqrt(input_dim))def forward (self, x: torch.Tensor ) -> torch.Tensor:return x @ self .weightclass Cruncher (nn.Module):def __init__ (self, dim: int , num_layers: int ):super ().__init__()self .layers = nn.ModuleList([for i in range (num_layers)self .final = Linear(dim, 1 )def forward (self, x: torch.Tensor ) -> torch.Tensor:for layer in self .layers:self .final(x)assert x.size() == torch.Size([B, 1 ])1 )assert x.size() == torch.Size([B])return x
记住要将模型移至 GPU。
1 2 3 4 5 6 7 8 9 device = get_device()8 assert y.size() == torch.Size([B])
3.3 Training loop and best practices
3.3.1 note about randomness
随机性出现在很多地方:参数初始化、dropout、数据排序等。
为了 <span style="color:red;">可复现性,建议 <span style="color: lightgreen;">在每次使用随机性时都传入不同的随机种子。
确定性在调试时特别有用,这样你可以追查 bug。
有三个地方需要设置随机种子,为了安全起见,你应该一次性全部设置。
1 2 3 4 5 6 7 8 9 10 11 0 import numpy as npimport random
3.3.2 data loading
在语言建模中,数据是整数序列(由 tokenizer 输出)。
将它们序列化为 numpy 数组很方便(由 tokenizer 完成)。
1 2 orig_data = np.array([1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ], dtype=np.int32)"data.npy" )
你可以将它们作为 numpy 数组加载回来。
不想一次性将整个数据加载到内存中(LLaMA 数据有 2.8TB),使用 memmap 仅惰性地将被访问的部分加载到内存中。
1 2 data = np.memmap("data.npy" , dtype=np.int32)assert np.array_equal(data, orig_data)
数据加载器生成用于训练的一批序列。
1 2 3 4 B = 2 4 assert x.size() == torch.Size([B, L])
3.3.3 optimizer
回顾我们的深度线性模型。
1 2 3 4 B = 2 4 2
让我们定义 AdaGrad 优化器
momentum = SGD + 梯度的指数平均
AdaGrad = SGD + 按 grad 2 \text{grad}^2 grad 2
RMSProp = AdaGrad + grad 2 \text{grad}^2 grad 2
Adam = RMSProp + momentum
AdaGrad: [paper]
1 2 optimizer = AdaGrad(model.parameters(), lr=0.01 )
计算梯度
1 2 3 4 5 x = torch.randn(B, D, device=get_device())4. , 5. ], device=get_device())input =pred_y, target=y)
执行一步
1 2 optimizer.step()
释放内存(可选)
1 optimizer.zero_grad(set_to_none=True )
下面是 AdaGrad 的一个实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class SGD (torch.optim.Optimizer):def __init__ (self, params: Iterable[nn.Parameter], lr: float = 0.01 ):super (SGD, self ).__init__(params, dict (lr=lr))def step (self ):for group in self .param_groups:"lr" ]for p in group["params" ]:class AdaGrad (torch.optim.Optimizer):def __init__ (self, params: Iterable[nn.Parameter], lr: float = 0.01 ):super (AdaGrad, self ).__init__(params, dict (lr=lr))def step (self ):for group in self .param_groups:"lr" ]for p in group["params" ]:self .state[p]"g2" , torch.zeros_like(grad))"g2" ] = g21e-5 )
3.3.3.1 内存
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 assert num_parameters == get_num_parameters(model)4 * (num_parameters + num_activations + num_gradients + num_optimizer_states)
3.3.3.2 计算(单步)
1 flops = 6 * B * num_parameters
Transformer 的计算更复杂,但思路是一样的。作业 1 会要求你完成这个计算。
3.3.4 train_loop
生成来自权重为 ( 0 , 1 , 2 , . . . , D − 1 ) (0, 1, 2, ..., D-1) ( 0 , 1 , 2 , ... , D − 1 )
1 2 3 4 5 6 D = 16 def get_batch (B: int ) -> tuple [torch.Tensor, torch.Tensor]:return (x, true_y)
让我们进行一次基础运行
1 train("simple" , get_batch, D=D, num_layers=0 , B=4 , num_train_steps=10 , lr=0.01 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def train (name: str , get_batch, D: int , num_layers: int , B: int , num_train_steps: int , lr: float ):0 ).to(get_device())0.01 )for t in range (num_train_steps):True )
进行一些超参数调优
1 train("simple" , get_batch, D=D, num_layers=0 , B=4 , num_train_steps=10 , lr=0.1 )
3.3.5 checkpointing
训练语言模型需要很长时间,而且肯定会崩溃。你不会想丢失所有的进度。
在训练过程中,定期将模型和优化器状态保存到磁盘是很有用的。
1 2 model = Cruncher(dim=64 , num_layers=3 ).to(get_device())0.01 )
保存检查点 (save the checkpoint)
1 2 3 4 5 6 checkpoint = {"model" : model.state_dict(),"optimizer" : optimizer.state_dict(),"model_checkpoint.pt" )
加载检查点 (load the checkpoint)
1 loaded_checkpoint = torch.load("model_checkpoint.pt" )
3.3.6 mixed precision training
数据类型(float32、bfloat16、fp8)的选择存在权衡。
更高精度:更准确/稳定,内存占用更多,计算量更大
更低精度:准确性/稳定性更差,内存占用更少,计算量更小
我们如何能兼顾两者的优势?
解决方案:默认使用 float32,但在可能的情况下使用 {bfloat16、fp8}。
一个具体方案:
PyTorch 有一个自动混合精度(AMP)库。
NVIDIA 的 Transformer Engine 支持线性层使用 FP8
在整个训练过程中广泛使用 FP8 [Peng+ 2023]
通常情况下,训练模型时,我们会采用更常规的浮点精度。在推理阶段,就可以使用各种“激进”的量化技术得到性能提升。