DDBM（上）

引入

标准的扩散模型：将高斯噪声映射为数据。

<span style="color:red">问题：如果先验是非高斯的，例如图像编辑(image editing)任务，应当如何处理？

分析：这类任务的目标是在成对图像之间建立映射。

相关探索

1. 对模型进行条件约束 (Ho and Salimans, 2022;Saharia et al., 2021) 或手动修改采样过程 (Meng et al., 2022; Song et al., 2020b)

   这些方法缺乏理论原则性，且仅实现单向映射（从受损图像到清晰图像），丧失了循环一致性条件 (cycle-consistency condition)。

2. 考虑直接对两个任意概率分布之间的传输过程进行建模。

   基于 ODE 的流匹配方法 (Lipman et al., 2023;Albergo and Vanden-Eijnden, 2023; Liu et al., 2022a) 学习两个任意概率分布之间的确定性路径，这类方法主要应用于图像生成问题，尚未在图像翻译任务中得到研究。此外，在图像生成方面，ODE方法尚未取得与扩散模型相当的实证成果。

3. 薛定谔桥 (De Bortoli et al., 2021) 学习两个概率分布之间的熵最优传输，但这类模型依赖昂贵的迭代近似方法。包括扩散桥匹配 (Shi et al., 2023; Peluchetti, 2023) 在内的最新扩展方法同样需要昂贵的迭代计算。

引入

Stanford 的 Linqi Zhou 等人提出一种可扩展的替代方案，以统一基于扩散的无条件生成方法和基于传输的分布转换方法，并将这一通用框架命名为 去噪扩散桥模型^[1] (Denoising Diffusion Bridge Models, DDBMs)。

本文从扩散桥的反向时间视角出发——扩散桥是一种以给定端点为条件的扩散过程，并基于这一角度建立了分布转换的通用框架。

具体而言，我们利用这一点来推广和改进架构预条件 (architecture pre-conditioning)、噪声调度 (noise schedule) 和模型采样器 (model sampler)，从而降低输入敏感性并提升性能稳定性。

随后，我们分别使用 DDBMs 在像素空间和潜空间上的模型来处理高维图像。对于标准图像翻译任务，DDBMs 在图像质量 (以FID指标衡量) 和翻译保真度 (以LPIPS、MSE为衡量指标) 上均取得更优结果。此外，如果将问题简化为图像生成任务，其性能与标准扩散模型相当。

实证研究中，我们将DDBMs应用于像素空间和潜空间中的复杂图像数据集。在标准图像平移任务上，DDBMs较基线方法取得显著提升；当将源分布设为噪声以简化为图像生成任务时，DDBMs在FID指标上仍能达到与最先进方法相当的水平，尽管其设计初衷是解决更通用的任务。

知识准备

2.1 扩散模型下的生成式建模

<span style = "color:red">生成模型的本质：将数据分布 $q_{\text{data}}(\mathbf{x})$ 逐步转换为先验分布 $p_{\text{prior}}(\mathbf{x})$，再通过学习逆转这一过程，进而从先验分布中采样并生成逼真样本。

扩散过程

该过程由一组时间索引变量 $\{\mathbf{x}_t\}_{t=0}^T$ 表示，其中

$$\begin{equation*} \mathbf{x}_0 \sim p_0(\mathbf{x}) := q_{\text{data}}(\mathbf{x}), \quad \mathbf{x}_T \sim p_T(\mathbf{x}) := p_{\text{prior}}(x) \end{equation*}$$

该过程可建模为如下SDE的解：

$$\begin{equation} d\mathbf{x}_t = \mathbf{f}(\mathbf{x}_t, t)dt + g(t)d\mathbf{w}_t \end{equation}$$

其中，

• $\mathbf{f}: \mathbb{R}^d \times [0, T] \to \mathbb{R}^d$ 是向量值漂移(drift)函数，
• $g: [0, T] \to \mathbb{R}$ 是标量值扩散系数，
• $\mathbf{w}_t$ 是 Wiener 过程。

沿着时间正向进行该扩散过程，会约束最终变量 $\mathbf{x}_T$ 服从先验分布 $p_{\text{prior}}(\mathbf{x})$。该过程的反向过程由下式给出：

$$\begin{equation} d\mathbf{x}_t = \left(\mathbf{f}(\mathbf{x}_t, t) - g(t)^2 \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)\right)dt + g(t)d\mathbf{w}_t \end{equation}$$

其中，$p(\mathbf{x}_t) := p(\mathbf{x}_t, t)$ 是 $\mathbf{x}_t$ 在时间 $t$ 时刻的边缘分布。

此外，还可推导出一个与上式具有相同边缘分布的等效确定性过程，称为 <span style="color:cyan">概率流ODE (probability flow ODE)：

$$\begin{equation} d\mathbf{x}_t = \left[\mathbf{f}(\mathbf{x}_t, t) - \frac{1}{2}g(t)^2 \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)\right]dt \end{equation}$$

特别地，可从 $\mathbf{x}_T \sim q_{\text{data}}(y)$ 中采样，并通过反向求解上述 反向SDE 或 ODE 来对 $q_{\text{data}}$ 进行采样。

去噪分数匹配

分数 $\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)$ 可通过分数匹配损失来学习：

$$\begin{equation} \mathcal{L}(\theta) = \mathbb{E}_{\mathbf{x}_t \sim p(\mathbf{x}_t | \mathbf{x}_0), \mathbf{x}_0 \sim q_{\text{data}}(\mathbf{x}), t \sim \mathcal{U}(0, T)} \left[\left\| s_\theta(\mathbf{x}_t, t) - \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t | \mathbf{x}_0) \right\|^2 \right] \end{equation}$$

使得上述损失的极小值 $s_\theta^*(\mathbf{x}_t, t)$ 能够逼近真实分数。关键在于，上述损失是易于处理的，因为转移核 $p(\mathbf{x}_t | \mathbf{x}_0)$ （其依赖于漂移函数和扩散函数的具体选取）被设计为高斯分布 $\mathbf{x}_t = \alpha_t \mathbf{x}_0 + \sigma_t \epsilon$，其中 $\alpha_t$ 和 $\sigma_t$ 是时间的函数，且 $\epsilon \sim N(0, I)$。通常也从 $\mathbf{x}_t$ 的信噪比（SNR）角度理解扩散过程，信噪比定义为

$$SNR = \alpha_t^2 / \sigma_t^2$$

2.2 具有固定端点的扩散过程

<span style="color:red">Doob’s h-transform： 可将 任意SDE 变成一个过定点 $\mathbf{x}_T$ 的扩散桥

去噪扩散桥模型示意图

DDBM采用由 <span style="color:lightblue">漂移调整(drift adjustment) 引导的扩散过程，朝向终点 $\mathbf{x}_T = y$。该模型通过匹配 <span style="color:orange">去噪桥分数(denoising bridge score) 来学习逆转此类桥接过程，从而允许从任意 $\mathbf{x}_T = y \sim q_{\text{data}}(y)$ 状态逆向恢复到 $\mathbf{x}_0$。顶部展示的前向SDE过程是单向的，而底部展示的概率流ODE则是 确定性的双向过程。白色节点为随机节点，灰色节点为确定性节点。

Stochastic bridges via h-transform

式 <a href="#eq:example" class="equation-ref">(1)</a> 所定义的扩散过程可通过 Doob’s h-transform 几乎必然地到达特定目标点 $y \in \mathbb{R}^d$：

$$\begin{equation} d\mathbf{x}_t = f(\mathbf{x}_t, t)dt + g(t)^2 \mathbf{h}(\mathbf{x}_t, t, y, T) + g(t)d\mathbf{w}_t, \quad \mathbf{x}_0 \sim q_{\text{data}}(x), \, \mathbf{x}_T = y \end{equation}$$

其中，

$$\begin{equation*} \mathbf{h}(x, t, y, T) = \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_T | \mathbf{x}_t) \big|_{\mathbf{x}_t=x, \mathbf{x}_T=y} \end{equation*}$$

表示原始 SDE 生成的从 $t$ 时刻到 $T$ 时刻的 对数转移核 在点 $\mathbf{x}_t = x$ 和 $\mathbf{x}_T = y$ 处的梯度，且每个 $\mathbf{x}_t$ 都显式依赖于 $T$ 时刻的 $y$。

此外，条件概率 $p(\mathbf{x}_T = y | \mathbf{x}_t)$ 满足Kolmogorov backward方程。在选择特定的漂移项和扩散项（例如 $\mathbf{f}(\mathbf{x}_t, t) = \mathbf{0}$）时，由于基础扩散过程具有可处理的（高斯）转移核，$\mathbf{h}$ 函数也易于求解(tractable)。

当初始点 $\mathbf{x}_0$ 固定时，该过程通常被称为 <span style="color:cyan">扩散桥，其能够将任意给定的 $\mathbf{x}_0$ 连接至给定的 $\mathbf{x}_T$，这一特性在图像到图像的翻译任务中极具应用前景。更值得注意的是，该转移核可能具有解析解，这为其应用提供了额外优势。

去噪扩散桥

3.1 时间反向SDE和概率流ODE

假设扩散桥的两个端点均存在于 $\mathbb{R}^d$ 中，且来自任意未知联合分布，即 $(\mathbf{x}_0, \mathbf{x}_T) = (\mathbf{x}, \mathbf{y}) \sim q_{\text{data}}(\mathbf{x}, y)$ ，我们希望设计一个过程：在给定从 $q_{\text{data}}(\mathbf{x}, \mathbf{y})$ 中抽取的成对样本训练集的情况下，通过学习反向具有边界分布 $q_{\text{data}}(\mathbf{x}, \mathbf{y})$ 的扩散桥，实现从 $q_{\text{data}}(\mathbf{x} | \mathbf{y})$ 中近似采样的功能。

VE桥（左）和VP桥（右）及其SDE可视化（上）和ODE可视化（下）

受扩散桥的启发，我们构建了具有边缘分布 $q(\mathbf{x}_t)$ 的随机过程 $\{\mathbf{x}_t\}_{t=0}^T$，使 $q(\mathbf{x}_0, \mathbf{x}_T)$ 逼近 $q_{\text{data}}(\mathbf{x}_0, \mathbf{x}_T)$。逆转该过程相当于从 $q(\mathbf{x}_t | \mathbf{x}_T)$ 中采样，可以通过以下定理构建 $q(\mathbf{x}_t | \mathbf{x}_T)$ 的时间反向SDE/概率流ODE。

<span style="color:red">定理1：条件概率 $q(\mathbf{x}_t | \mathbf{x}_T)$ 的演化过程具有如下形式的时间反向SDE：

$$\begin{equation} d\mathbf{x}_t = \left[ \mathbf{f}(\mathbf{x}_t, t) - g^2(t) \left( \mathbf{s}(\mathbf{x}_t, t, y, T) - \mathbf{h}(\mathbf{x}_t, t, y, T) \right) \right] dt + g(t)d\hat{\mathbf{w}}_t, \, \mathbf{x}_T = y \end{equation}$$

及其相关的概率流ODE：

$$\begin{equation} d\mathbf{x}_t = \left[ \mathbf{f}(\mathbf{x}_t, t) - g^2(t) \left( \frac{1}{2}\mathbf{s}(\mathbf{x}_t, t, y, T) - \mathbf{h}(\mathbf{x}_t, t, y, T) \right) \right] dt, \, \mathbf{x}_T = y \end{equation}$$

对于任意 $\epsilon > 0$ ，上述方程在 $t \leq T - \epsilon$ 上成立，其中 $\hat{w}_t$ 表示Wiener过程， $\mathbf{s}(x, t, y, T) = \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t | \mathbf{x}_T) \big|_{\mathbf{x}_t=x, \mathbf{x}_T=y}$ ，且 $\mathbf{h}$ 如式 <a href="#eq:5" class="equation-ref">(5)</a> 所定义。

特别地，上述过程的定义到 $T - \epsilon$ 为止。

1. 在SDE情况下，为恢复初始分布，做近似 $\mathbf{x}_{T-\epsilon} \approx y$（$\epsilon$为小量），并反向模拟SDE。
2. 在ODE情况下，需要从 $p(\mathbf{x}_{T-\epsilon})$ 中采样。可先近似 $\mathbf{x}_{T-\epsilon^\prime} \approx y$（其中 $\epsilon > \epsilon^\prime > 0$），再通过 Euler-Maruyama 步得到 $\mathbf{x}_{T-\epsilon}$，然后用式 进行求解。

3.2 边缘分布与去噪桥分数匹配

<a href="#thm:1" class="equation-ref">定理1</a> 中的采样过程需要对分数

$$\begin{equation*} \mathbf{s}(x, t, y, T)=\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t | \mathbf{x}_T)|_{\mathbf{x}_t=x, \mathbf{x}_T=y} \end{equation*}$$

进行近似，其中

$$\begin{equation*} q(\mathbf{x}_t | \mathbf{x}_T)=\int_{\mathbf{x}_0} q(\mathbf{x}_t | \mathbf{x}_0, \mathbf{x}_T) q_{\text{data}}(\mathbf{x}_0 | \mathbf{x}_T)d\mathbf{x}_0 \end{equation*}$$

由于真实分数没有闭式解，此处使用神经网络来近似真实分数。这通常会产生给定数据时 $\mathbf{x}_t$ 的闭式边缘采样（例如，在扩散模型中为 $\mathbf{x}_0$，在我们的情况下为 $(\mathbf{x}_0, \mathbf{x}_T)$），并且给定 $\mathbf{x}_t$ 时，模型通过训练以匹配闭式去噪分数目标。我们倾向于采用类似的方法，原因在于：

1. $\mathbf{x}_t$ 的边缘采样易于处理；
2. 闭式目标使得算法简单且可扩展。

我们详细说明如何设计边缘采样分布和易处理的分数目标，以近似真实的条件分数 $\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t | \mathbf{x}_T)$。

关键点1：采样分布

对前一点，设计采样分布 $q(\cdot)$，使 $q(\mathbf{x}_t | \mathbf{x}_0, \mathbf{x}_T):=p(\mathbf{x}_t | \mathbf{x}_0, \mathbf{x}_T)$，其中 $p(\cdot)$ 是如式 <a href="#eq:5" class="equation-ref">(5)</a> 所示的固定在两个端点的扩散分布。对于具有高斯转移核的扩散过程（例如VE、VP），我们的采样分布是如下形式的高斯分布：

$$\begin{align} q(\mathbf{x}_t | \mathbf{x}_0, \mathbf{x}_T)&=\mathcal{N}(\hat{\mu}_t, \hat{\sigma}_t^2 I), \text{其中} \notag\\ \hat{\mu}_t&=\frac{SNR_T}{SNR_t} \cdot \frac{\alpha_t}{\alpha_T} \mathbf{x}_T + \alpha_t \mathbf{x}_0 \left(1-\frac{SNR_T}{SNR_t}\right) \\ \hat{\sigma}_t^2&=\sigma_t^2 \left(1-\frac{SNR_T}{SNR_t}\right) \notag \end{align}$$

其中 $\alpha_t$ 和 $\sigma_t$ 是预定义的信号和噪声调度， $SNR_t=\alpha_t^2 / \sigma_t^2$ 是时间 $t$ 处的信噪比。对于VE调度，我们假设 $\alpha_t=1$，推导细节见附录A.1。值得注意的是，该分布的均值是（经缩放的）端点之间的线性插值，且当接近任一端点时，该分布趋近于 Dirac 分布。

关键点2：训练目标

对后一点，扩散桥得益于与扩散模型类似的设置，因为预定义的信号/噪声调度会产生闭式条件分数 $\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t | \mathbf{x}_0, \mathbf{x}_T)$。我们在下面的定理中表明，当 $\mathbf{x}_t \sim q(\mathbf{x}_t | \mathbf{x}_0, \mathbf{x}_T)$ 时，与该闭式分数匹配的神经网络 $s_\theta(\mathbf{x}_t, \mathbf{x}_T, t)$ 能够近似真实分数。

<span style="color:red">定理2：(Denoising Bridge Score Matching) 设 $(\mathbf{x}_0, \mathbf{x}_T) \sim q_{\text{data}}(\mathbf{x}, \mathbf{y})$，$\mathbf{x}_t \sim q(\mathbf{x}_t | \mathbf{x}_0, \mathbf{x}_T)$，$t \sim p(t)$。其中 $p(t)$ 是 $[0, T]$ 上任意非零时间采样分布，且 $w(t)$ 是任意非零损失权重项。则以下目标的最小值：

$$\begin{equation} \mathcal{L}(\theta)=\mathbb{E}_{\mathbf{x}_t, \mathbf{x}_0, \mathbf{x}_T, t}\left[w(t)\left\|s_\theta(\mathbf{x}_t, \mathbf{x}_T, t)-\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t | \mathbf{x}_0, \mathbf{x}_T)\right\|^2\right] \end{equation}$$

满足 $s_\theta(\mathbf{x}_t, \mathbf{x}_T, t)=\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t | \mathbf{x}_T)$。

简而言之，我们在两个端点上建立了一个易处理的扩散桥，并且通过匹配高斯桥的条件分数，我们能够学习满足边界分布 $q_{\text{data}}(x, y)$ 的新分布 $q(\mathbf{x}_t | \mathbf{x}_T)$ 的分数。

分布转换的广义参数化

将桥过程建立在扩散过程之上，使我们能够将分数网络参数化 $s_\theta(\mathbf{x}_t, \mathbf{x}_T, t)$

EDM（Karras等人，2022）提出将模型输出参数化为

$$\begin{equation*} D_\theta(\mathbf{x}_t, t) = c_{\text{skip}}(t)\mathbf{x}_t + c_{\text{out}}(t)F_\theta(c_{\text{in}}(t)\mathbf{x}_t, c_{\text{noise}}(t)) \end{equation*}$$

其中 $F_\theta$ 是一个带有参数 $\theta$ 的神经网络，用于预测 $\mathbf{x}_0$。本着类似的精神，我们采用这种 pred-x 参数化，并额外推导出一组用于分布转换的缩放函数，我们证明这是 EDM 参数化的严格超集。

分数重参数化

遵循式 <a href="#eq:8" class="equation-ref">(8)</a> 中提出的采样分布，pred-x模型可以通过以下方式预测桥分数：

$$\begin{equation} \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t | \mathbf{x}_T) \approx -\frac{\mathbf{x}_t - \left( \frac{SNR_T}{SNR_t} \cdot \frac{\alpha_t}{\alpha_T} \mathbf{x}_T + \alpha_t D_\theta(\mathbf{x}_t, \mathbf{x}_T, t) \left(1 - \frac{SNR_T}{SNR_t}\right) \right)}{\sigma_t^2 \left(1 - \frac{SNR_T}{SNR_t}\right)} = \frac{b_t D_\theta(\mathbf{x}_t, \mathbf{x}_T, t) + a_t \mathbf{x}_T - \mathbf{x}_t}{c_t} \end{equation}$$

$$\nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t | \mathbf{x}_T) \approx \frac{b_t D_\theta(\mathbf{x}_t, \mathbf{x}_T, t) + a_t \mathbf{x}_T - \mathbf{x}_t}{c_t}$$

缩放函数和损失权重

借鉴 Karras 等人（2022）的研究，令

$$\begin{equation*} a_t = \frac{\alpha_t}{\alpha_T} \cdot \frac{SNR_T}{SNR_t}, \quad b_t = \alpha_t(1 - \frac{SNR_T}{SNR_t}), \quad c_t = \sigma_t^2(1 - \frac{SNR_T}{SNR_t}) \end{equation*}$$

可推导出缩放函数和权重函数 $w(t)$ 如下：

$$\begin{align} &c_{\text{in}}(t) = \frac{1}{\sqrt{a_t^2 \sigma_T^2 + b_t^2 \sigma_0^2 + 2a_t b_t \sigma_{0T} + c_t}}, \ c_{\text{out}}(t) = \sqrt{a_t^2 (\sigma_T^2 \sigma_0^2 - \sigma_{0T}^2) + \sigma_0^2 c_t} \times c_{\text{in}}(t) \\ &c_{\text{skip}}(t) = \left( b_t \sigma_0^2 + a_t \sigma_{0T} \right) \times c_{\text{in}}^2(t), \ w(t) = \frac{1}{c_{\text{out}}(t)^2}, \ c_{\text{noise}}(t) = \frac{1}{4} \log(t) \end{align}$$

其中，$\sigma_0^2$、$\sigma_T^2$ 和 $\sigma_{0T}$ 分别表示 $\mathbf{x}_0$ 的方差、$\mathbf{x}_T$ 的方差以及两者的协方差。

与EDM相比，唯一额外的超参数是 $\sigma_T$ 和 $\sigma_{0T}$，它们描述了 $\mathbf{x}_T$ 的分布及其与 $\mathbf{x}_0$ 的相关性。可以注意到，在EDM的情况下，$\sigma_t = t$，$\sigma_T^2 = \sigma_0^2 + T^2$（因为对于某些高斯噪声 $\epsilon$，$\mathbf{x}_T = \mathbf{x}_0 + T\epsilon$），$\sigma_{0T} = \sigma_0^2$，且 $SNR_T/SNR_t = t^2/T^2$。

可以证明，此时的缩放函数会简化为EDM中的缩放函数。详细推导见附录A.5。

广义时间反演 Generalized time-reversal

由于概率流ODE与分类器引导（Dhariwal和Nichol，2021；Ho和Salimans，2022）存在相似性，我们可以引入一个额外的参数 $w$ 来设置漂移调整的“强度”，如下所示：

$$\begin{equation} d\mathbf{x}_t = \left[ \mathbf{f}(\mathbf{x}_t, t) - g^2(t) \left( \frac{1}{2} \mathbf{s}(\mathbf{x}_t, t, y, T) - w \mathbf{h}(\mathbf{x}_t, t, y, T) \right) \right] dt, \quad \mathbf{x}_T = y \end{equation}$$

这使得由此产生的概率流ODE能够生成范围更广的 $\mathbf{x}_t$ 边缘密度。我们将在消融研究中考察该参数的影响。

去噪扩散桥的随机采样

使用纯粹ODE路径的<span style="color:red">问题： 扩散桥具有给定数据的固定起点 $\mathbf{x}_T = y \sim q_{\text{data}}(y)$，而沿概率流 ODE 反向时间演化会生成一条确定性 “期望” 路径，这可能导致输出变得 “平均化”。

解决方法：在采样过程中引入噪声，以提高采样质量和多样性。

高阶混合采样器。我们的采样器基于先前的高阶 ODE 采样器（Karras 等人，2022）构建，该采样器将采样步骤离散化为具有递减间隔的 $t_N > t_{N-1} > \cdots > t_0$（详见附录 A.6）。受 Song 等人（2020b）提出的预测 - 校正采样器的启发，我们在高阶 ODE 步骤之间额外引入了一个按计划执行的Euler-Maruyama步，该步骤遵循反向随机微分方程（SDE）。这确保了每一步的边缘分布大致保持不变。我们引入额外的缩放超参数s，其定义了 $t_{i-1}$ 和 $t_i$ 之间的步长比例，使得区间 $[t_i - s(t_i - t_{i-1}), t_i]$ 用于 Euler-Maruyama 步，而 $[t_{i-1}, t_i - s(t_i - t_{i-1})]$ 用于 Heun 步，如算法 1 所述。

去噪扩散桥混合采样器

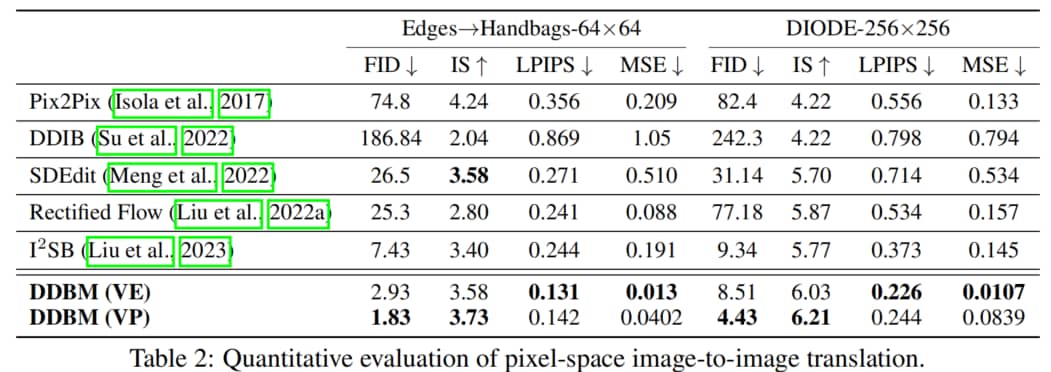
像素空间图像翻译任务的定量评估

消融实验

无条件图像生成的性能评估

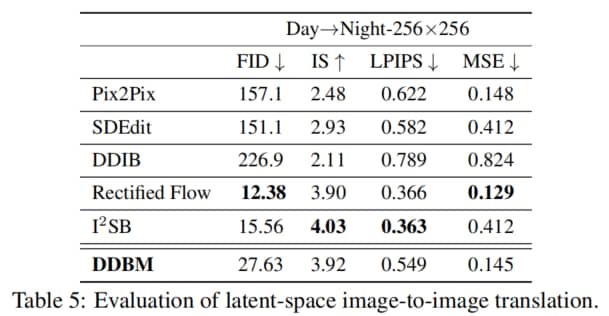
（日→夜）隐空间上的图像生成

Edges→Handbags示例

DIODE示例

6 相关工作与特殊情况

相关工作

扩散模型。扩散模型的进展（Sohl-Dickstein等人，2015；Ho等人，2020；Song等人，2020b）提升了图像生成的最先进水平，并超越了生成对抗网络（GANs）（Goodfellow等人，2014）。扩散模型的成功与其重要的设计选择密不可分，例如网络设计（Song等人，2020b；Karras等人，2022；Nichol和Dhariwal，2021；Hoogeboom等人，2023；Peebles和Xie，2023）、改进的噪声调度（Nichol和Dhariwal，2021；Karras等人，2022；Peebles和Xie，2023）、更快更准确的采样器（Song等人，2020a；Lu等人，2022a；b；Zhang和Chen，2022）以及引导方法（Dhariwal和Nichol，2021；Ho和Salimans，2022）。鉴于关于无条件生成的扩散模型已有大量文献，且这些文献在很大程度上基于上述各种设计选择，我们旨在设计我们的桥模型公式，以实现与这些文献的无缝整合。为此，我们采用时间反转的视角来直接扩展这些方法。

扩散桥、薛定谔桥与杜布h变换。扩散桥（Särkkä和Solin，2019）是概率论中的常用工具，近年来在生成建模领域得到了积极研究（Liu等人，2022b；Somnath等人，2023；De Bortoli等人，2021；Peluchetti；2023）。Heng等人（2021）研究了以固定起点/终点为条件的扩散桥，并在给定分数∇ₓᵗlog p(xₜ)近似的情况下，学习模拟桥的时间反转过程。最近，Liu等人（2022b）不再考虑具有固定端点的桥，而是利用杜布h变换在任意分布之间构建桥。通过在训练过程中模拟整个路径并进行分数匹配，学习正向桥。相比之下，其他工作（Somnath等人，2023；Peluchetti）虽然也采用杜布h变换，但提出了用于正向时间生成的无模拟算法。Delbracio和Milanfar（2023）同样构建了用于直接迭代的布朗桥，并成功应用于图像恢复任务。另一种方法是De Bortoli等人（2021）提出的迭代比例拟合（IPF），用于高效解决不同分布间转换的薛定谔桥（SB）问题。Liu等人（2023）基于一类可处理的薛定谔桥，提出了一种无模拟算法，并在图像翻译任务中表现出优异性能。最近，通过IPF扩展薛定谔桥，桥匹配（Shi等人，2023）提出使用迭代马尔可夫拟合来解决薛定谔桥问题。Peluchetti（2023）也开发了一种类似的算法用于分布转换。与我们的工作更相关的是Li等人（2023）的研究，其提出在离散时间中直接反转布朗桥以实现分布转换。而我们的方法则展示了如何在连续时间中基于现有的VP和VE扩散过程构建桥模型，且大多数先前工作中考虑的布朗桥只是VE桥的一个特例。我们还证明，若实现得当，VP桥能取得非常优异的实证性能。尽管Peluchetti的研究中也采用正向时间扩散的视角，并提出了VE/VP桥调度，但我们的框架具有额外的实证优势（可复用扩散模型的设计）和理论优势（与OT流匹配（Lipman等人，2023；Tong等人，2023b）及整流流（Liu等人，2022a）相关联）。

流与最优传输。基于流匹配的工作（Lipman等人，2023；Tong等人，2023b；Pooladian等人，2023；Tong等人，2023a）学习基于ODE的传输映射，以连接两个分布。Lipman等人（2023）证明，通过匹配预定义传输映射的速度场，可构建与扩散模型相当的强大生成模型。为改进这一方法，Tong等人（2023b）、Pooladian等人（2023）利用小批量无模拟最优传输（OT）来挖掘分布间的潜在耦合。整流流（Liu等人，2022a）直接构建最优传输桥，并使用神经网络拟合中间速度场。另一类工作利用随机插值（Albergo和Vanden-Eijnden，2023）构建流模型，直接避免使用杜布h函数，并提供了一种简便的分布间插值映射构建方法。Albergo等人（2023）提出了基于随机插值的通用理论，统一了流模型和扩散模型，并表明可从ODE和SDE两种视角构建桥。与这些方法不同，我们的模型采用了与这类模型不同的去噪桥分数匹配损失。从这一视角出发，我们能够将扩散模型中许多已被证实成功的设计（这些设计无法直接应用于上述工作）扩展到桥框架中，在推动图像翻译任务达到新高度的同时，保持在无条件生成任务中的优异性能。

6.1 去噪扩散桥模型的特殊情况

情况1：无条件扩散过程

对于无条件扩散过程（将数据映射到噪声），我们首先可以证明，当 $\mathbf{x}_T \sim q_{\text{data}}(y | x) = \mathcal{N}(\alpha_T x, \sigma_T^2 I)$ 时，若 $p(\mathbf{x}_0) = q_{\text{data}}(x)$ ，则边缘分布 $p(\mathbf{x}_t)$ 与常规扩散过程的边缘分布完全匹配。通过对式 中的 $\mathbf{x}_T$ 求期望，我们得到：

$$\begin{equation} p(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}(\alpha_t \mathbf{x}_0, \sigma_t I) \end{equation}$$

进一步可以证明，当从高斯分布中采样 $\mathbf{x}_T$ 时，采样过程中式 和式 会分别简化为扩散过程的反向SDE和ODE。推导细节详见附录A.4。

情况2：OT-Flow Matching and Rectified Flow

OT流匹配（Lipman等人，2023；Tong等人，2023b）和整流流（Liu等人，2022a）。这些工作学习匹配通过ODE（而非SDE）定义的确定性动态。在这种特定情况下，它们处理由 $\mathbf{x}_T - \mathbf{x}_0$ 定义的“直线”路径。

为说明我们的框架对这类方法的泛化性，首先定义一族扩散桥，其方差由 $c \in (0,1)$ 缩放，即 $p(\mathbf{x}_t | \mathbf{x}_0, \mathbf{x}_T) = \mathcal{N}(\hat{\mu}_t, c^2 \hat{\sigma}_t^2 I)$，其中 $\hat{\mu}_t$ 和 $\hat{\sigma}_t$ 如式 所定义。由此可以证明，对于VE扩散（其中 $\sigma_t^2 = c^2 t$），给定固定的 $\mathbf{x}_0$ 和 $\mathbf{x}_t$（即 $T=1$），且 $\mathbf{x}_t$ 从式 中采样时：

$$\begin{equation} \lim_{c \to 0} \left[ f(\mathbf{x}_t, t) - c^2 g^2(t) \left( \frac{1}{2} \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t | \mathbf{x}_0, \mathbf{x}_1) - \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_1 | \mathbf{x}_t) \right) \right] = \mathbf{x}_1 - \mathbf{x}_0 \end{equation}$$

图3：与最相关基线方法的定性比较。

其中，括号内的项是给定 $\mathbf{x}_0$ 和 $\mathbf{x}_1$ 时式 中概率流ODE的漂移项，右侧则恰好是直线路径项。换句话说，这些方法在无噪声极限下学习匹配（具有特定VE调度的）桥概率流ODE的漂移项。此时，分数模型可与 $\mathbf{x}_T - \mathbf{x}_0$ 匹配，再加上一些处理额外输入 $\mathbf{x}_T$ 的注意事项，我们的框架便完全简化为OT流匹配和整流流的框架（详见附录A.4）。

参考文献

• [1] Denoising Diffusion Bridge Models
  Zhou, L., Lou, A., Khanna, S., & Ermon, S. ICLR 2024, https://arxiv.org/abs/2309.16948.
• [2] Diffusion Bridge Implicit Models
  Zheng, K., He, G., Chen, J., Bao, F., & Zhu, J. ICLR 2025, https://arxiv.org/abs/2405.15885.
• [3] Reverse-time diffusion equation models
  B.D. Anderson. Stochastic Processes and their Applications, Vol 12(3), pp. 313--326. Elsevier. 1982.