EDM：扩散模型的设计空间（上）

2025/08/04 - 至今
待完善

主要参考资料

本篇文章主要基于《Elucidating the Design Space of Diffusion-Based
Generative Models》以及以下几个视频、博文。

数学推导参考：B站讲解 Double童发发 - EDM论文讲解之扩散模型通用框架系列、苏剑林-科学空间-一般框架之SDE篇

整体脉络、相关图片参考：B站讲座 -【双语】NVIDIA - EDM 以及 论文相关博文

本文按照上述讲座顺序，分为四个部分：

• 第一部分：通用框架
  • 识别现有研究中的可变部分
• 第二部分：确定性采样
  • 高效求解 ODE
• 第三部分：随机采样
  • 为什么用 SDE？如何进行随机步长计算？
• 第四部分：预处理与训练
  • 如何训练用于评估单步的卷积神经网络（CNN）？

核心问题：如何将Diffusion Models表达在一个统一框架下？

回顾

• Score Matching
  • 加噪公式：$\mathbf{x}_t = \mathbf{x}_0 + \sigma_t \varepsilon$
  • 概率分布形式：$p(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t;\mathbf{x}_0,\sigma_t^2 \mathbf{I})$
• Flow Matching
  • 加噪公式：$\mathbf{x}_t = (1-t) \mathbf{x}_0 + t \varepsilon$
  • 概率分布形式：$p(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; (1-t)\mathbf{x}_0, t^2 \mathbf{I})$
• DDPM/DDIM
  • 加噪公式：$\mathbf{x}_t = \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t} \varepsilon$
  • 概率分布形式：$p(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1-\bar{\alpha}_t)\mathbf{I})$

Song等人将其 前向SDE 定义为：

$$\mathrm{d}\boldsymbol{x} = \boldsymbol{f}(\boldsymbol{x}, t)\mathrm{d}t + g(t)\mathrm{d}\omega_t$$

其中

• $\omega_t$ 是标准Wiener过程；
• $\boldsymbol{f}(\cdot, t): \mathbb{R}^d \to \mathbb{R}^d$ 为漂移系数；
• $g(\cdot): \mathbb{R} \to \mathbb{R}$ 为扩散系数
• $d$ 为数据集维度。

在 方差保持（VP） 和 方差爆炸（VE） 公式中，这两个系数的选择不同；且 $\boldsymbol{f}(\cdot, t)$ 始终具有 $\boldsymbol{f}(\boldsymbol{x}, t) = f(t)\boldsymbol{x}$ 的形式（其中 $f(\cdot): \mathbb{R} \to \mathbb{R}$）。因此，该SDE可等价改写为：

$$\mathrm{d}\boldsymbol{x} = f(t)\boldsymbol{x}\mathrm{d}t + g(t)\mathrm{d}\omega_t$$

该SDE的扰动核具有如下一般形式：

$$p_{0t}(\boldsymbol{x}(t) \mid \boldsymbol{x}(0)) = \mathcal{N}\big(\boldsymbol{x}(t);\ s(t)\boldsymbol{x}(0),\ s^2(t)\sigma^2(t)\boldsymbol{I}\big)$$

其中 $\mathcal{N}(\boldsymbol{x};\ \boldsymbol{\mu},\ \boldsymbol{\Sigma})$ 表示均值为 $\boldsymbol{\mu}$、协方差为 $\boldsymbol{\Sigma}$ 的高斯分布在 $\boldsymbol{x}$ 处的概率密度函数，且：

$$s(t) = \exp\left( \int_0^t f(\xi)\mathrm{d}\xi \right), \quad \sigma(t) = \sqrt{ \int_0^t \frac{g^2(\xi)}{s^2(\xi)} \mathrm{d}\xi }$$

边缘分布 $p_t(\boldsymbol{x})$ 可通过对初始状态 $\boldsymbol{x}(0)$ 积分扰动核得到：

$$p_t(\boldsymbol{x}) = \int_{\mathbb{R}^d} p_{0t}(\boldsymbol{x} \mid \boldsymbol{x}_0)\, p_{\text{data}}(\boldsymbol{x}_0)\,\mathrm{d}\boldsymbol{x}_0$$

Song等人定义了 概率流ODE，使采样出的 $\boldsymbol{x}$ 服从上述相同的边缘分布 $p_t(\boldsymbol{x})$：

$$\mathrm{d}\boldsymbol{x} = \left[ f(t)\boldsymbol{x} - \frac{1}{2}g(t)^2 \nabla_{\boldsymbol{x}} \log p_t(\boldsymbol{x}) \right] \mathrm{d}t$$

通过连续时间随机过程将数据扰动至纯噪声

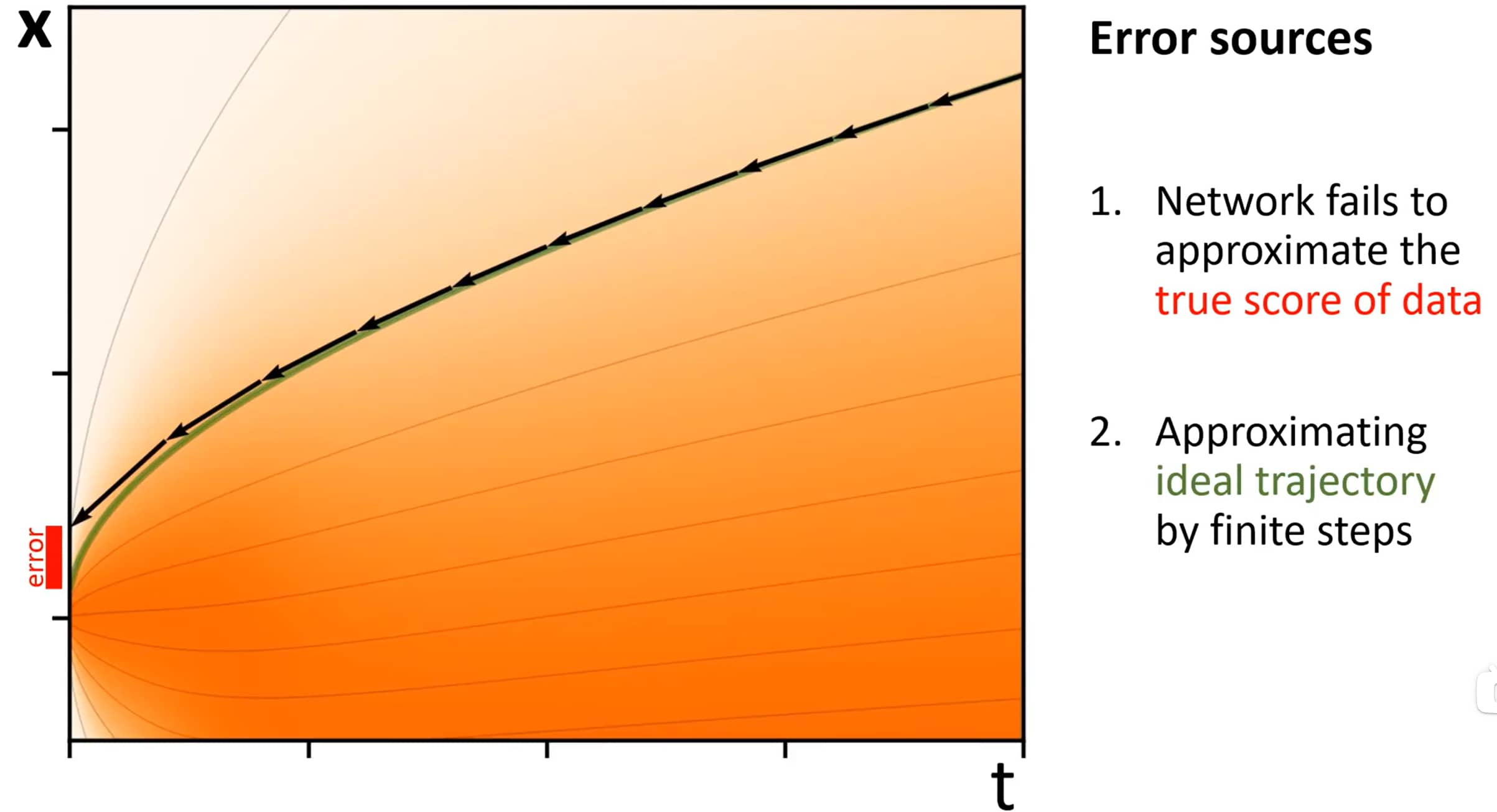
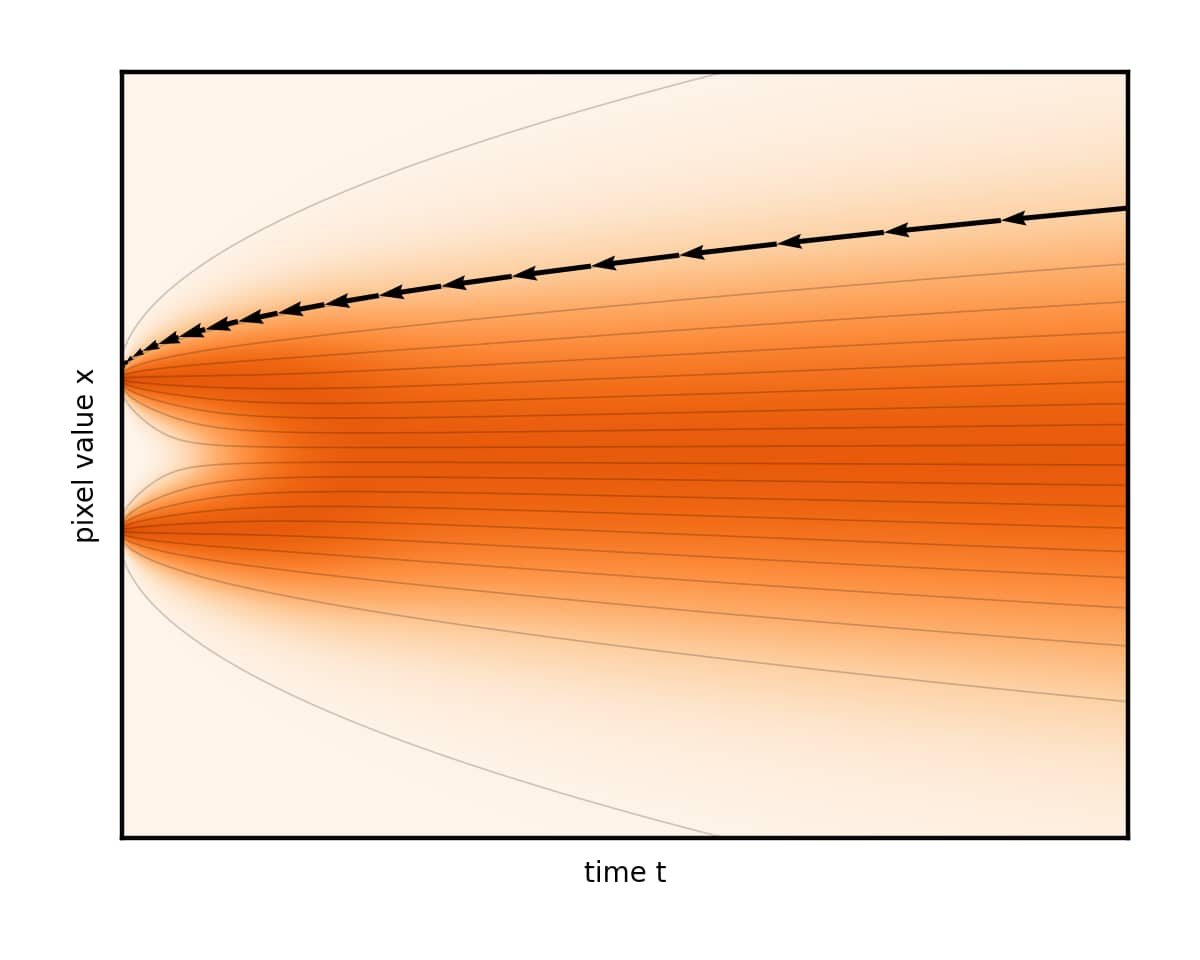
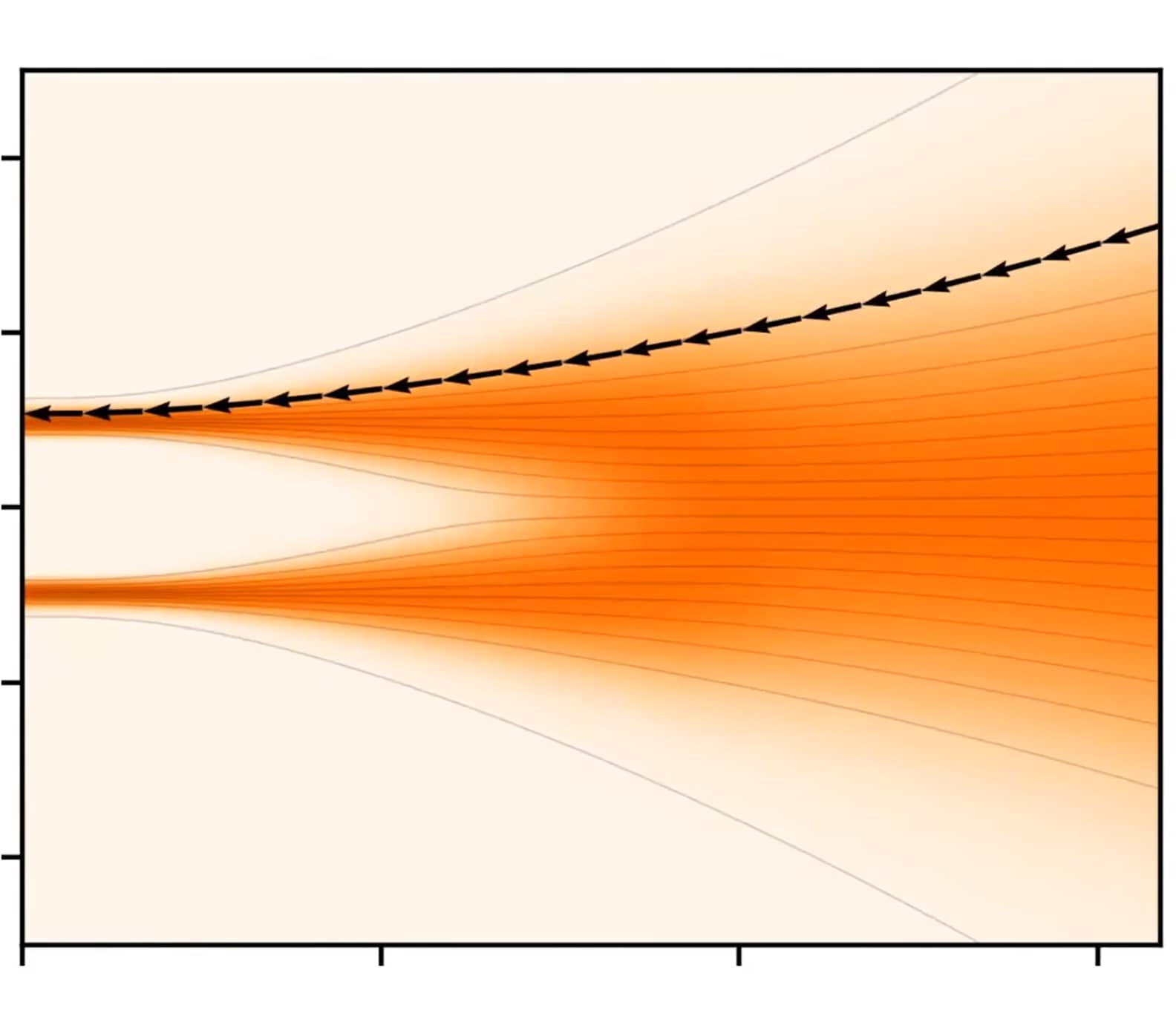
SDE视角下，扩散模型出现的两个问题

1. 网络无法逼近数据的 真实得分：这导致采样轨迹朝着错误方向演进。上图当前轨迹（黑色）为错误采样链，在左侧与目标之间存在error；
2. 通过有限步长逼近 理想轨迹：为了近似绿色轨迹，如果每步太长，则会显著偏离目标轨迹；如果每步太短，则会消耗过多计算资源。

事实上，以上两点分别对应于 Traning过程 和 Sampling过程。

轨迹

确定性采样的改进

基于ODE的确定性采样

不改变训练过程，只关注于采样过程。

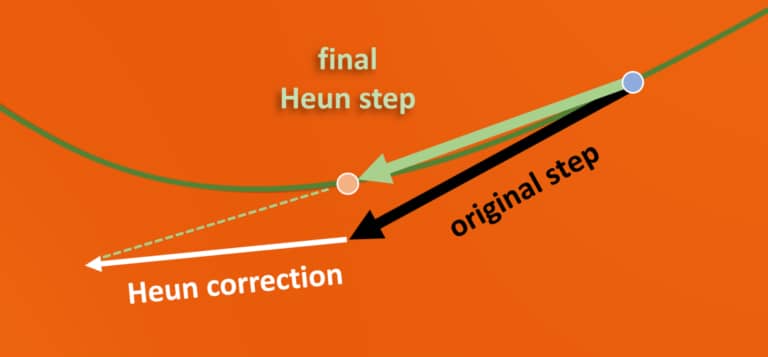
改进Heun步

概率流ODE的改造

原始ODE公式围绕函数 $f$ 和 $g$ 构建，这两个函数直接对应公式中的特定项；而边缘分布的性质只能通过这些函数 间接推导。由于概率流ODE的核心是边缘分布，所以我们的目标是 直接基于 $\sigma(t)$ 和 $s(t)$ 定义ODE。

概率流ODE的核心特征是：若将服从分布 $p(x_a;\sigma(t_a))$ 的样本 $x_a$ 从时刻 $t_a$ 演化到时刻 $t_b$（无论时间正向还是反向），最终得到的样本 $x_b$ 会服从分布 $p(x_b;\sigma(t_b))$。参考现有研究，该特性可通过以下方程满足（详细推导见《EDM-下》）：

$$dx = -\dot{\sigma}(t)\sigma(t)\nabla_x \log p(x;\sigma(t))dt \tag{1}$$

其中，符号“$\dot{}$”表示对时间的导数。$\nabla_x \log p(x;\sigma)$ 是得分函数，它是一个向量场，在给定噪声水平下始终指向数据密度更高的方向。从直观上理解，该ODE的无穷小正向步会将样本推离数据分布，其推移速率取决于噪声水平的变化；反之，反向步则会将样本推向数据分布。

关键事实：概率流ODE的每一种具体形式，本质上都是同一标准ODE的重新参数化；改变 $\sigma(t)$ 对应于对时间 $t$ 的重新参数化，而改变 $s(t)$ 则对应于对变量 $\boldsymbol{x}$ 的重新参数化。

去噪得分匹配

提出一种 $D_\theta$ 以统一 Score-Based Model的 $s_\theta$、DDPM/DDIM的 $\varepsilon_\theta$ 和 Flow Matching的 $v_\theta$

假设 $D(\boldsymbol{x};\sigma)$ 是一种去噪网络，$\boldsymbol{x} = \boldsymbol{y} + \boldsymbol{n}$ 是加噪后的图像，$\boldsymbol{y}$ 是原始图像， $\boldsymbol{n}$ 是噪声，$\sigma$ 是噪声水平。对每个 $\sigma$ 分别最小化从 $p_{data}$ 中抽取样本的预期 $L_2$ 去噪误差，即：

$$\mathbb{E}_{\boldsymbol{y} \sim p_{data}} \mathbb{E}_{\boldsymbol{n} \sim \mathcal{N}(0,\sigma^2 I)} \|D(y + n;\sigma) - y\|_2^2 \tag{2}$$

有，

$$\nabla_x \log p(x;\sigma) = \frac{D(x;\sigma) - x}{\sigma^2} \tag{3}$$

出噪声成分，而式 <a href="#eq:1">(1)</a> 会随时间对该噪声成分进行放大（或减弱）。

图1展示了理想状态下 $D$ 在实际应用中的表现。扩散模型的核心发现是：$D(x;\sigma)$ 可通过神经网络 $D_\theta(x;\sigma)$ 实现，且该神经网络能依据式 <a href="#eq:2">(2)</a> 进行训练。需注意，$D_\theta$ 可能包含额外的预处理与后处理步骤（例如将 $x$ 缩放到合适的动态范围）；我们将在第5节中回到此类预处理相关的讨论。

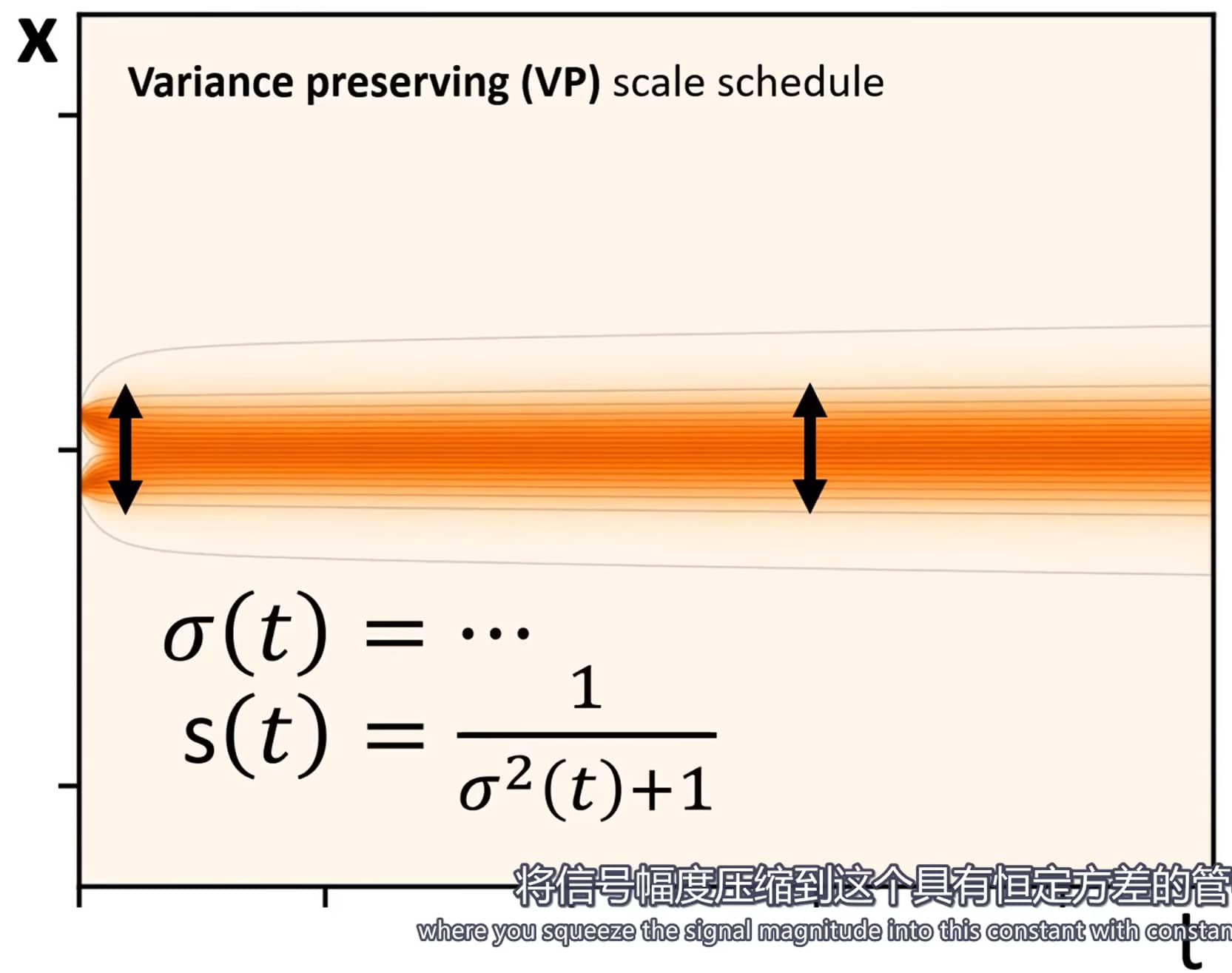
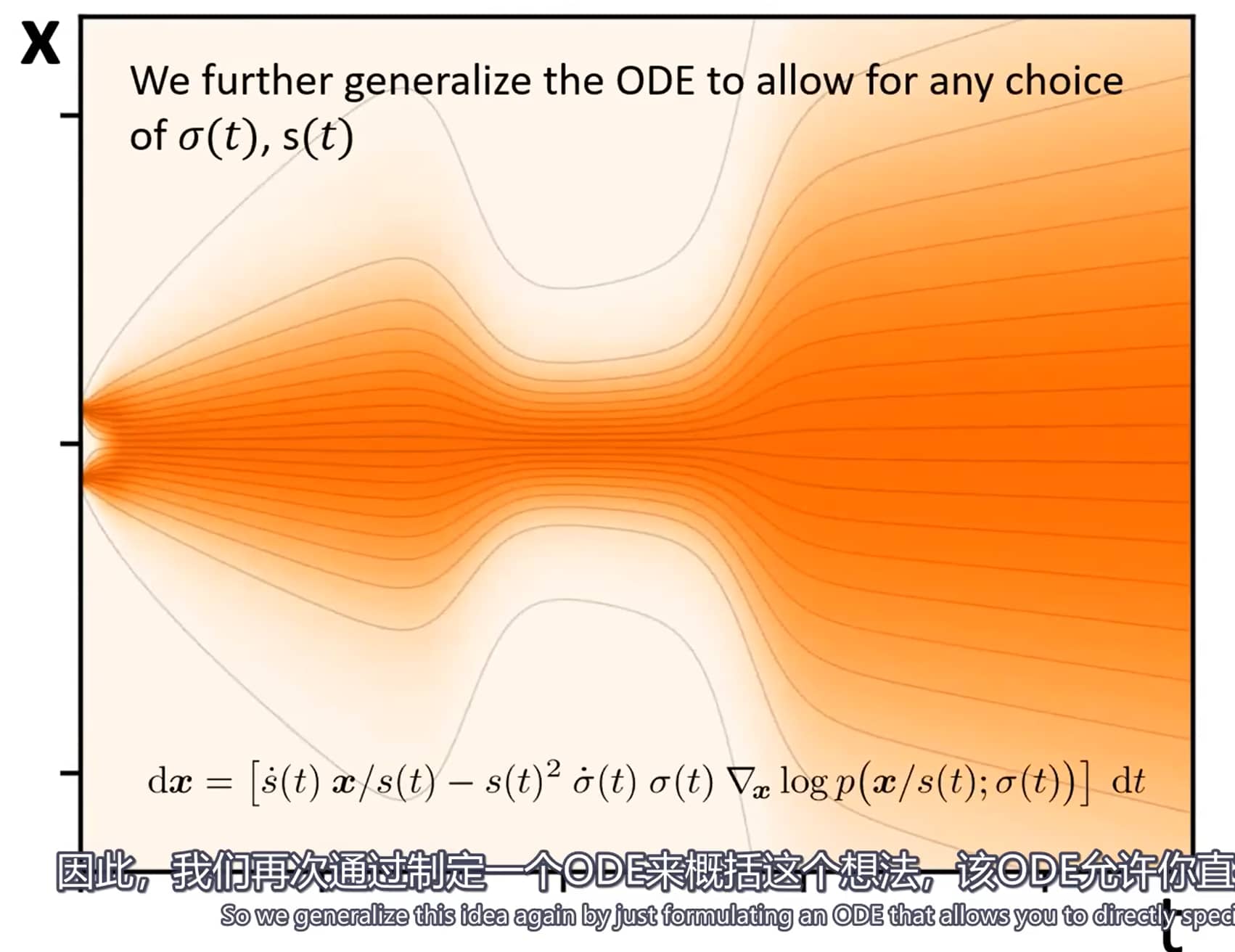
与时间相关的信号缩放

部分方法（见附录C.1）会引入额外的缩放调度函数 $s(t)$，并将 $x = s(t)\hat{x}$ 视为原始非缩放变量 $\hat{x}$ 的缩放版本。这一操作会改变与时间相关的概率密度，进而改变ODE的解轨迹。由此得到的ODE是式 <a href="#eq:1">(1)</a> 的推广形式：

$$dx = \left[ \frac{\dot{s}(t)}{s(t)} x - s(t)^2 \dot{\sigma}(t) \sigma(t) \nabla_x \log p\left( \frac{x}{s(t)} ; \sigma(t) \right) \right] dt \tag{4}$$

需注意，在评估得分函数时，我们会显式取消对 $x$ 的缩放操作，以确保 $p(x;\sigma)$ 的定义与 $s(t)$ 无关。

在扩散模型研究中，提升采样输出质量和/或降低采样计算成本是常见的研究方向。我们的假设是：与采样过程相关的选择在很大程度上独立于其他组件，例如网络架构和训练细节。换句话说，$D_\theta$ 的训练过程不应决定 $\sigma(t)$、$s(t)$ 和 $\{t_i\}$ 的选择，反之亦然；从采样器的角度来看，$D_\theta$ 就是一个黑箱。

为验证这一假设，我们在三个预训练模型上评估了不同的采样器，每个模型分别代表一种不同的理论框架和模型类别。我们首先使用这些模型的原始采样器实现来测量基准结果，然后利用表1中的公式将这些采样器纳入我们的统一框架，之后再应用我们提出的改进方案。这使我们能够评估不同的实际选择方案，并提出适用于所有模型的采样过程通用性改进。

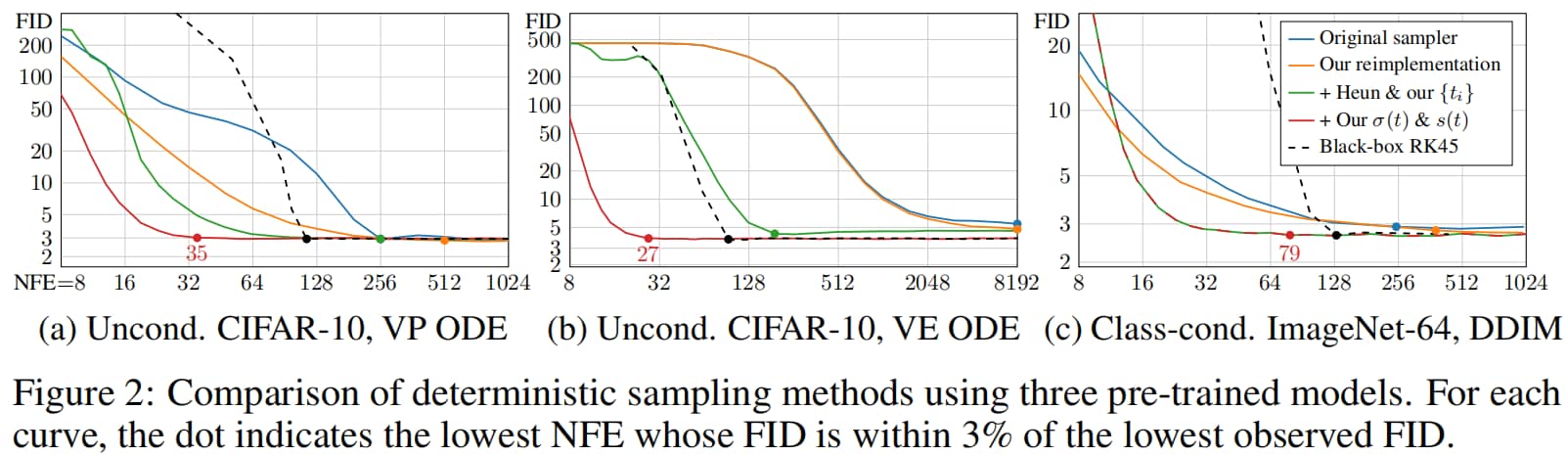
我们以弗雷歇初始距离（Fréchet Inception Distance, FID）[15]作为结果质量的评估指标，该指标通过计算50000张生成图像与所有可用真实图像之间的距离得到。图2展示了FID随神经函数评估次数（Neural Function Evaluations, NFE）变化的情况，其中NFE指生成单张图像所需的 $D_\theta$ 评估次数。由于采样过程的成本完全由 $D_\theta$ 的计算成本主导，因此NFE的降低会直接转化为采样速度的提升。

原始确定性采样器的结果以蓝色显示，而这些方法在我们统一框架中的重新实现版本（橙色）得到了相近但始终更优的结果。这种差异源于原始实现中的某些疏漏，以及我们在DDIM（模型）情况下对离散噪声水平的更细致处理；具体参见附录C。需注意，尽管各原始代码库的结构差异很大，但我们的重新实现版本完全由算法1和表1定义。

离散化与高阶积分器

待求解的ODE可通过将式（3）代入式（4）得到——此举可定义逐点梯度，而ODE的解可通过数值积分求得，即对离散时间区间取有限步长。这一过程需同时选择积分方案（如欧拉法或龙格-库塔法的变体）与离散采样时间 $\{t_0, t_1, \dots, t_N\}$。此前的诸多研究依赖欧拉法，但我们将在第3节中证明：二阶求解器能实现更优的计算权衡。为简洁起见，本文未单独提供欧拉法应用于该ODE的伪代码，但可通过省略算法1中的第6-8行得到。

==========================

对常微分方程（ODE）进行数值求解，本质上是对其真实解轨迹的近似。在每一步迭代中，求解器都会引入截断误差，该误差会在 $N$ 步迭代过程中累积。局部误差通常随步长超线性变化，因此增加迭代次数 $N$ 可以提高解的精度。

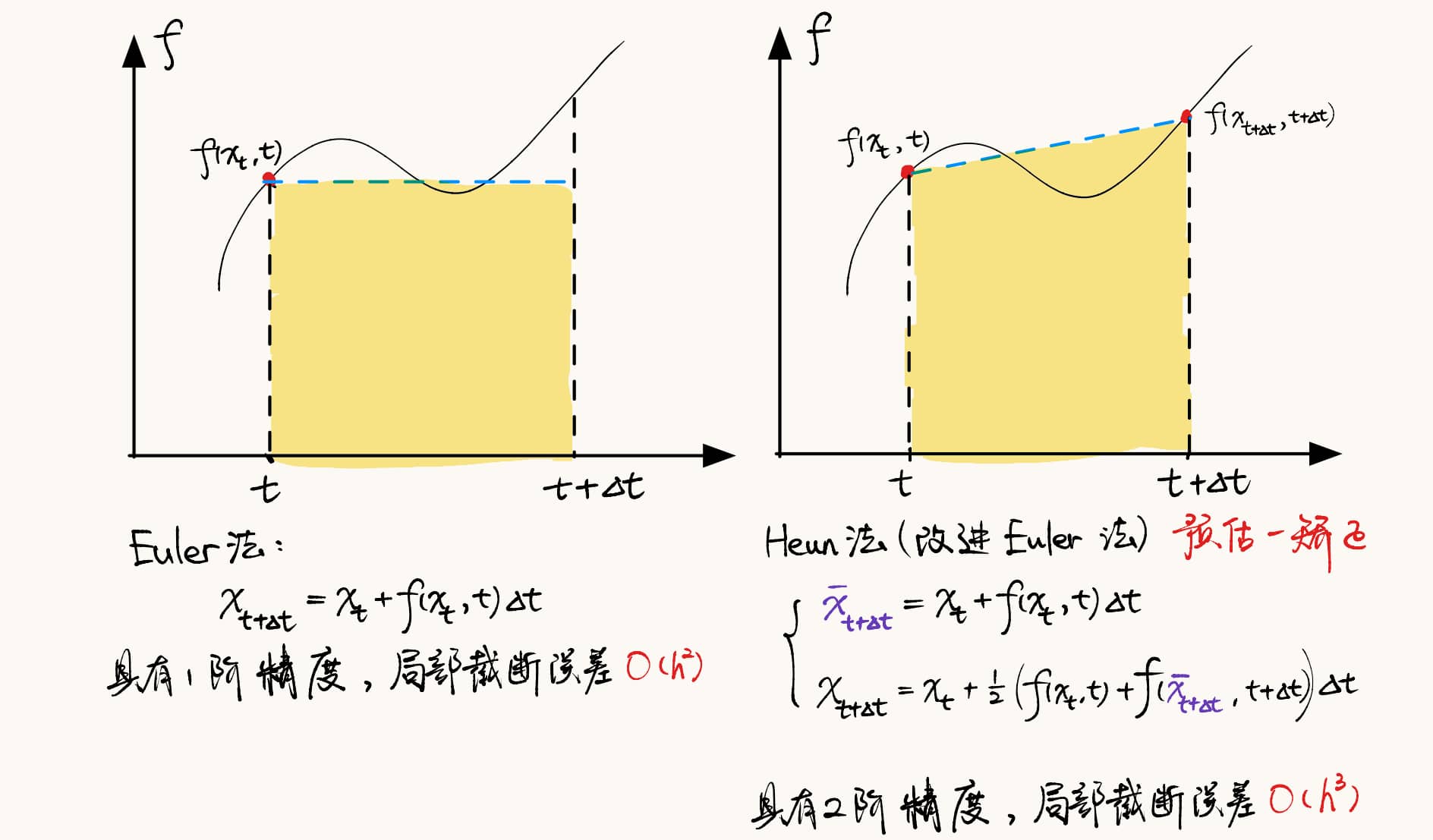
常用的欧拉法是一阶ODE求解器，其局部误差关于步长 $h$ 为 $O(h^2)$ 阶。高阶龙格-库塔法[50]的（误差）变化更优，但需要多次（调用神经函数）

使用二阶Heun步的确定性采样算法

Euler法和Heun法

每一步都需要对 $D_\theta$ 进行多次评估。近期也有研究提出将线性多步法用于扩散模型的采样[31,59]。通过大量测试，我们发现Heun二阶方法[2]（又称改进欧拉法、梯形法则）——此前Jolicoeur-Martineau等人[24]已在扩散模型场景中对其进行过探索——在截断误差与神经函数评估次数（NFE）之间实现了极佳的权衡。

如算法1所示，该方法为 $x_{i+1}$ 引入了一个额外的校正步骤，以考虑 $t_i$ 到 $t_{i+1}$ 之间 $\frac{dx}{dt}$ 的变化。这一校正使局部误差达到 $O(h^3)$ 阶，但代价是每一步需额外对 $D_\theta$ 进行一次评估。需注意，当步进到 $\sigma=0$ 时会出现除以零的情况，因此在此场景下我们退回到欧拉法。

关于二阶求解器的通用类别，我们将在附录D.2中展开讨论。

时间步 $\{t_i\}$ 决定了步长的分配方式，进而决定了截断误差在不同噪声水平间的分布。我们在附录D.1中进行了详细分析，得出结论：步长应随 $\sigma$ 的减小而单调减小，且无需针对单个样本调整步长。

EDM 采用如下参数化方案：

缩放因子 $s(t) = 1$

噪声水平序列 $\{\sigma_i\}$ 按如下定义，

$$\sigma_{i<N} = \left( \sigma_{max}^{\frac{1}{\rho}} + \frac{i}{N-1} \left( \sigma_{min}^{\frac{1}{\rho}} - \sigma_{max}^{\frac{1}{\rho}} \right) \right)^\rho, \quad \sigma_N = 0 \tag{5}$$

其中，$\rho$ 用于控制“以 $\sigma_{max}$ 附近步长变长为代价，将 $\sigma_{min}$ 附近步长缩短多少”。实验结果表明：当 $\rho=3$ 时，各步的截断误差接近均等；但对于图像采样，$\rho$ 取5至10之间的值时性能会显著更优。这表明 $\sigma_{min}$ 附近的误差对采样质量影响更大。在本文后续内容中，我们将 $\rho$ 设为7。

改进后确定性采样方法的效果

Heun方法与式（5）的实验结果以图2中的绿色曲线展示。我们观察到所有场景下均有一致性提升：Heun方法能以显著更低的NFE达到与欧拉法相同的FID。

整合分析

表1给出了在本文框架下重现三种早期方法的确定性变体所需的公式。选择这些方法，一方面是因为它们应用广泛，另一方面，选择这些方法，不仅因为它们能实现最先进（state-of-the-art, SOTA）的性能，还因为它们源自不同的理论基础。我们的部分公式与原文献看起来差异较大，这是因为我们移除了其中的间接表述和递归结构；具体细节参见附录C。这种重新构建框架的主要目的，是清晰呈现此前研究中常相互纠缠的所有独立组件。在我们的框架中，组件之间不存在隐式依赖——原则上，对单个公式的任何选择（在合理范围内）都能得到一个可正常运行的模型。换句话说，修改某一个组件并不需要为了维持某项性质（例如模型在极限情况下收敛到数据分布）而对其他部分进行修改。当然，在实际应用中，某些选择和组合的效果必然会优于其他选择和组合。

---

随机采样

纠偏过程

确定性采样具有诸多优势，例如可通过反转ODE将真实图像转化为对应的 latent 表示（潜变量表示）。然而，与“每一步向图像中注入新噪声”的随机采样相比，确定性采样往往会导致更差的输出质量[47,49]。既然ODE与随机微分方程（SDE）在理论上可恢复相同的分布，那么随机性的具体作用究竟是什么？

研究背景

Song等人[49]提出的SDE可推广为[20,58]：概率流ODE（式1）与时变朗之万扩散（Langevin diffusion）SDE[14]之和（详见附录B.5），具体形式如下：

$$\mathrm{d}\boldsymbol{x}_\pm = \underbrace{ \textcolor{lime}{-\dot{\sigma}(t)\sigma(t)\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x}; \sigma(t)) \,\mathrm{d}t} }_{\text{概率流ODE}} \pm \underbrace{ \textcolor{orange}{\beta(t)\sigma(t)^2\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x}; \sigma(t)) \,\mathrm{d}t}}_{\substack{\text{确定性噪声衰减}}} + \underbrace{\textcolor{cyan}{\sqrt{2\beta(t)}\sigma(t) \,\mathrm{d}\omega_t} }_{\substack{\text{噪声注入}}} \tag{6}$$

其中，$\omega_t$ 为标准维纳过程（Wiener process）。$dx_+$ 与 $dx_-$ 分别对应时间正向和反向推移的独立SDE，二者通过Anderson时间反转公式[1]关联。

朗之万项可进一步拆解为“基于得分的确定性去噪项”与“随机性噪声注入项”，这两项对噪声水平的净贡献相互抵消。由此，$\beta(t)$ 实质表示“现有噪声被新噪声替换的相对速率”。当选择 $\beta(t) = \dot{\sigma}(t)/\sigma(t)$ 时，可还原Song等人[49]提出的SDE——此时得分项会从正向SDE中消失。

这一视角揭示了随机性在实际应用中的作用：隐式朗之万扩散会在特定时刻将样本推向目标边际分布，主动修正早期采样步骤中产生的误差。但另一方面，用离散SDE求解器步骤近似朗之万项的过程本身也会引入误差。现有研究[3,24,47,49]表明，非零的 $\beta(t)$ 具有积极作用，但据我们观察，Song等人[49]中对 $\beta(t)$ 的隐式选择并无特殊性质。因此，随机性的最优强度需通过实验确定。

第一项

$-\dot{\sigma}(t)\sigma(t)\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x};\sigma(t))\mathrm{d}t$

这个部分就是EDM框架下的通用PDE/ODE形式，只是在 $s(t)=1$ 的情形下。这一部分的出现预示着基于逆向SDE的随机性采样过程也一定包含与确定性采样类似的过程。

第二项

$\pm \beta(t)\sigma^2(t)\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x};\sigma(t))\mathrm{d}t$

这一部分是确定性噪声衰减项，代入Score与单纯去噪模型 $D_\theta(\boldsymbol{x};\sigma)$ 的关系，有：

$$\begin{align*} \pm \beta(t)\sigma^2(t)\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x};\sigma(t))\mathrm{d}t &= \pm \beta(t)\sigma^2(t)\frac{D_\theta(\boldsymbol{x};\sigma(t)) - \boldsymbol{x}}{\sigma^2(t)}\mathrm{d}t \\ &= \pm \beta(t)\left( D_\theta(\boldsymbol{x};\sigma(t)) - \boldsymbol{x} \right)\mathrm{d}t \end{align*}$$

由于 $D_\theta(\boldsymbol{x};\sigma)$ 是单纯去噪模型，又有 $\boldsymbol{x} = \boldsymbol{y} + \boldsymbol{n}$，其中 $\boldsymbol{y}$ 为原始图像，$\boldsymbol{n}$ 为噪声，满足 $\boldsymbol{n} \sim \mathcal{N}(0, \sigma^2(t)\mathbf{I})$，有：

$$\pm \beta(t)\left( D_\theta(\boldsymbol{x};\sigma(t)) - \boldsymbol{x} \right) \approx \pm \beta(t)(\boldsymbol{y} - \boldsymbol{x})\mathrm{d}t = \mp \beta(t)\boldsymbol{n}\mathrm{d}t$$

也即，第二部分的值实际上与噪声水平成正比，噪声水平越大对 $\boldsymbol{x}$ 的改变越大。

第三项

$\sqrt{2\beta(t)}\sigma(t)\mathrm{d}w_t$

由于维纳过程 $\mathrm{d}w_t$ 的存在，这一项显然属于随机项，被称为随机噪声注入项。由于随机项的存在，在采样的同时需要“不断加噪”，可以认识是一种去噪过程的回退，往回退一点，再往前走，有助于修正之前采样过程存在的误差。

$$\begin{align*} \sqrt{2\beta(t)}\sigma(t)\mathrm{d}w_t &= \sqrt{2\beta(t)}\sigma(t)\boldsymbol{\varepsilon}\sqrt{\mathrm{d}t} \\ &= \sqrt{2\beta(t)}\boldsymbol{n}^\prime\sqrt{\mathrm{d}t} \end{align*}$$

这里，噪声 $\boldsymbol{n}$ 和 $\boldsymbol{n}^\prime$ 均服从分布 $\mathcal{N}(0, \sigma^2(t)\mathbf{I})$，但他们有本质的区别。其中 $\boldsymbol{n}$ 是采样图像当前存在的噪声，是确定值，但是维纳过程的 $\boldsymbol{\varepsilon}$ 是每一个采样步骤随机，所以二者噪声水平相当但不相等！联合公式(12)来看，对于加噪SDE有：

$$\beta(t)\sigma^2(t)\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x};\sigma(t))\mathrm{d}t + \sqrt{2\beta(t)}\sigma(t)\mathrm{d}w_t = -\beta(t)\boldsymbol{n}\mathrm{d}t + \sqrt{2\beta(t)}\boldsymbol{n}^\prime \sqrt{\mathrm{d}t}$$

观察公式(15)，在向前SDE当中，同时在进行着相同水平噪声的加噪和去噪过程，$\beta(t)$ 控制二者的相对速率。

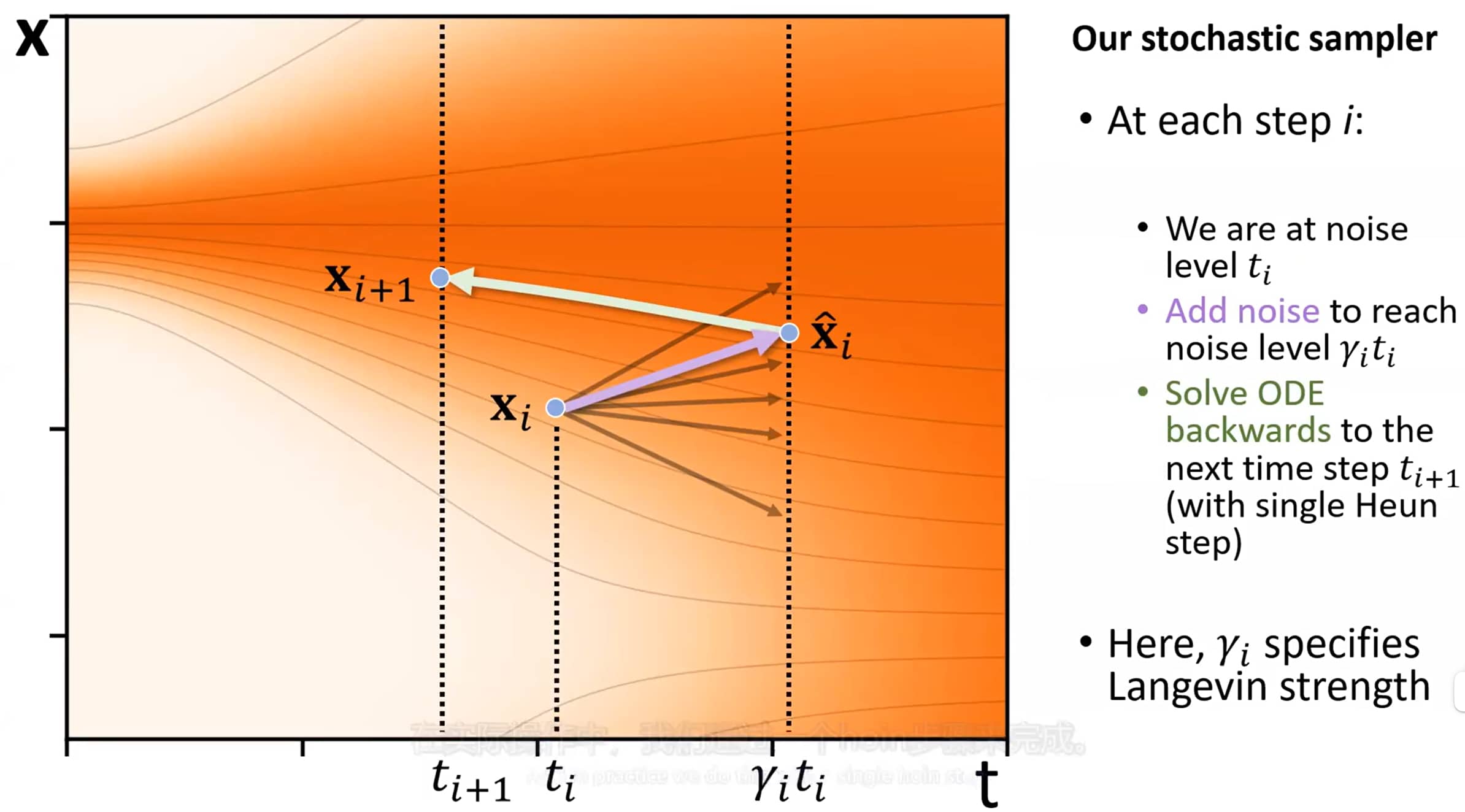
本文提出的随机采样器

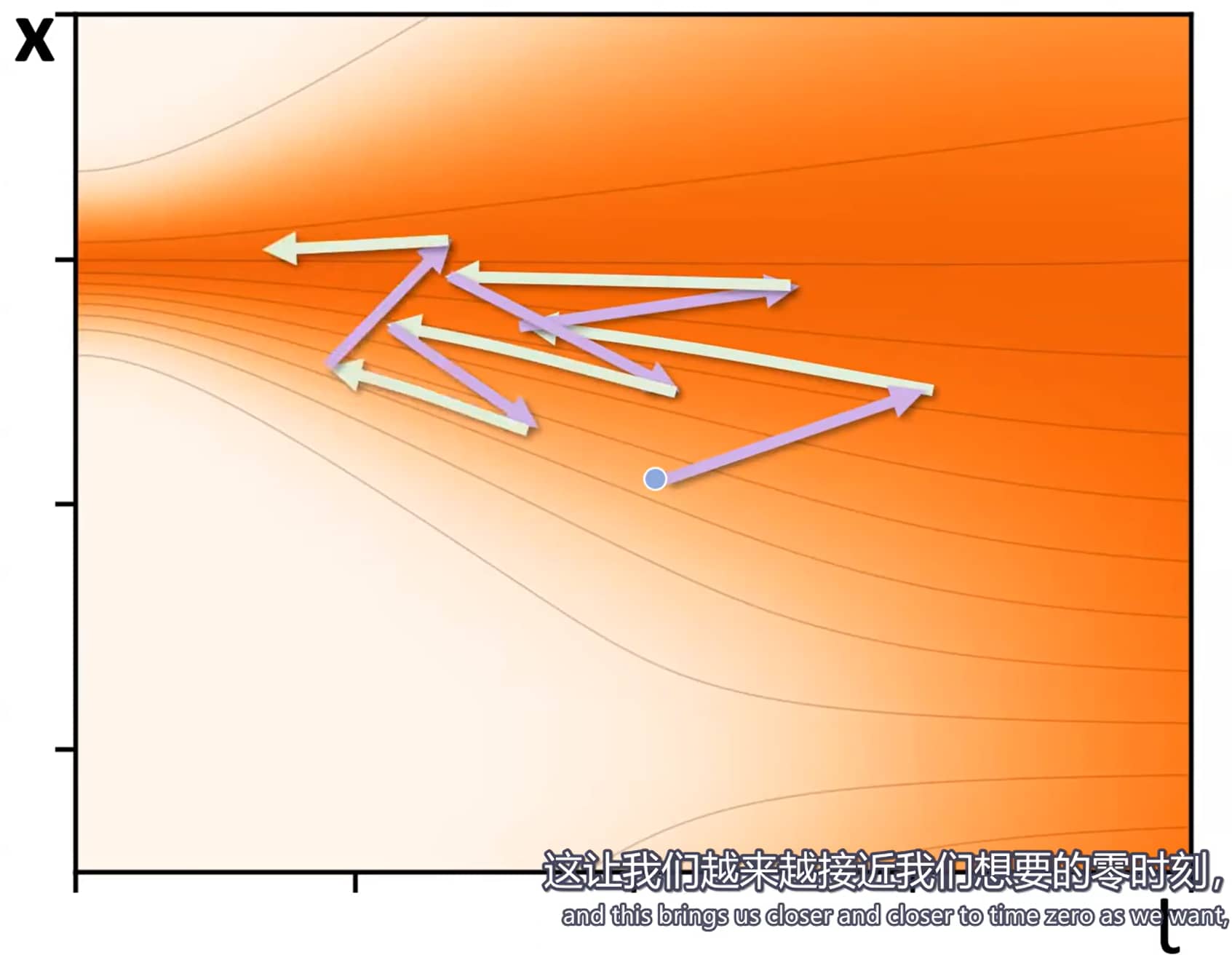
我们提出的随机采样器，将二阶确定性ODE积分器与“添加-移除噪声”的显式朗之万式“扰动（churn）”相结合，伪代码详见算法2。在每一步 $i$ 中，给定噪声水平 $t_i$（即 $\sigma(t_i)$）下的样本 $x_i$，我们执行两个（步骤）子步骤

EDM随机采样器具体算法

第一步，根据系数 $\gamma_i \geq 0$ 向样本中添加噪声，使噪声水平提升至 $\hat{t}_i = t_i + \gamma_i t_i$；第二步，从噪声水平提升后的样本 $\hat{x}_i$ 出发，通过单步反向求解常微分方程（ODE），将噪声水平从 $\hat{t}_i$ 降至 $t_{i+1}$。由此得到噪声水平为 $t_{i+1}$ 的样本 $x_{i+1}$，之后继续迭代这一过程。

需强调的是，该方法并非通用的随机微分方程（SDE）求解器，而是针对该特定问题定制的采样流程。其正确性源于两个子步骤的交替执行——每个子步骤均能维持正确的分布（ODE步骤中存在的截断误差除外）。Song等人[49]提出的预测-校正采样器，与本文方法在概念结构上具有相似性。

Q：为什么要控制 $\gamma_i \leq \sqrt{2}-1$ ？

A：这是为了加噪水平不至于太大，导致远离正确采样路径。

比如，令 $\varepsilon_i \sim \mathcal{N}(0, \sigma^2(t_i)\mathbf{I})$，当 $\gamma_i = \sqrt{2} - 1$ 时，有：

$$\hat{t_i} = t_i + \gamma_i t_i = t_i + (\sqrt{2} - 1) t_i = \sqrt{2} t_i$$

于是

$$\hat{x_i} = x_i + \sqrt{\hat{t_i}^2 - t_i^2} = x_i + t_i \varepsilon_i$$

其中，$x_i \sim \mathcal{N}(x,t_i^2 \ \mathbf{I})$（$x$ 为真实值），$t_i \varepsilon_i \sim \mathcal{N}(0, t_i^2 \ \mathbf{I})$

本文方法与欧拉-丸山法的核心差异分析

我们首先注意到：欧拉-丸山法在对式（6）进行离散化时，存在一个细微偏差。可将欧拉-丸山法理解为“先添加噪声，再执行ODE步”，但它并非从噪声注入后的中间状态开始执行ODE步，而是假设在迭代步骤初始时，$x$ 和 $\sigma$ 仍处于初始状态。

在我们的方法中，算法2第7行用于评估 $D_\theta$ 的参数对应噪声注入后的状态，而类似欧拉-丸山法的方法会使用 $x_i$、$t_i$，而非 $\hat{x}_i$、$\hat{t}_i$。当时间步长 $\Delta t$ 趋近于0时，这两种选择可能无差异；但当目标是用较大步长实现低神经函数评估次数（NFE）时，二者的差异会变得十分显著。

实际应用考量

增加随机性虽能有效校正早期采样步骤产生的误差，但也存在自身缺陷。我们观察到（详见附录E.1）：在所有数据集和去噪器网络中，过度执行类似朗之万过程的“噪声添加-移除”操作，会导致生成图像的细节逐渐丢失；此外，在噪声水平极低和极高的情况下，图像还会出现颜色过饱和的偏移问题。我们推测，实际应用中的去噪器会使式（3）中的向量场产生轻微的非保守性，这一现象违背了朗之万扩散的前提假设，进而导致上述不利影响。值得注意的是，我们使用解析去噪器（如图1b中的去噪器）进行的实验，并未出现此类质量退化问题。

若图像质量退化由 $D_\theta(x;\sigma)$ 的缺陷导致，则只能在采样过程中通过启发式方法弥补。针对颜色过饱和偏移问题，我们的解决方案是：仅在特定噪声水平范围 $t_i \in [S_{tmin}, S_{tmax}]$ 内启用随机性。对于该范围内的噪声水平，我们定义 $\gamma_i = S_{churn}/N$，其中 $S_{churn}$ 用于控制随机性的总体强度；同时，我们对 $\gamma_i$ 进行限制，确保新注入的噪声量不会超过图像中已有的噪声量。

最后，我们发现：将 $S_{noise}$ 设置为略大于1的值，以扩大新注入噪声的标准差，可在一定程度上抵消细节丢失问题。这一现象表明，$D_\theta(x;\sigma)$ 的非保守性（前文假设）主要体现为“去噪器倾向于移除过多噪声”——这很可能是由于任何基于 $L_2$ 损失训练的去噪器，都会不可避免地出现向均值回归的现象[30]。

随机采样超参示意图

• 发现一：小噪声水平过多次的随机噪声注入影响图像分布

  • 现象描述：当噪声水平低于 0.2 或者更低的时候，过多次的噪声注入会使得生成图像会出现过饱和现象，甚至完全被破坏，证明了SDE中的过分的随机噪声注入对生成过程没有好处。
  • 解决办法：设置一个 $s_{\text{tmin}} > 0$，当图像噪声水平已经足够小了，就不进行噪声注入，等价于采用确定性采样。

• 发现二：大噪声水平过多次的随机噪声注入影响图像分布

  • 现象描述：当噪声水平较高时，过多次的随机噪声注入会让图像变得抽象，背景变得色彩单调。
  • 解决办法：设置一个 $s_{\text{noise}}$，这个值略大于 1.0，但这个办法不能缓解发现一种的问题。

EDM随机采样参数设置

EDM采样总结

上图中，红色线代表确定性采样的结果，橙色线代表不采用 $S_{\text{tmin}}$ 和 $S_{\text{tmax}}$，绿色线代表不采用 $S_{\text{tmin}}$ 和 $S_{\text{tmax}}$，同时也不采用 $S_{\text{noise}}$，蓝色线代表不采用 $S_{\text{noise}}$，紫色线为最优设置。

1. 确定性采样可以在更短的时间达到更低的FID，表明可以加速采样
2. 随机性采样在更多步数以后可以达到更低的FID，效果比确定性采样要好
3. 随机性采样以超参数设置与更多迭代步数为代价，换来了更好的采样性能

评估结果

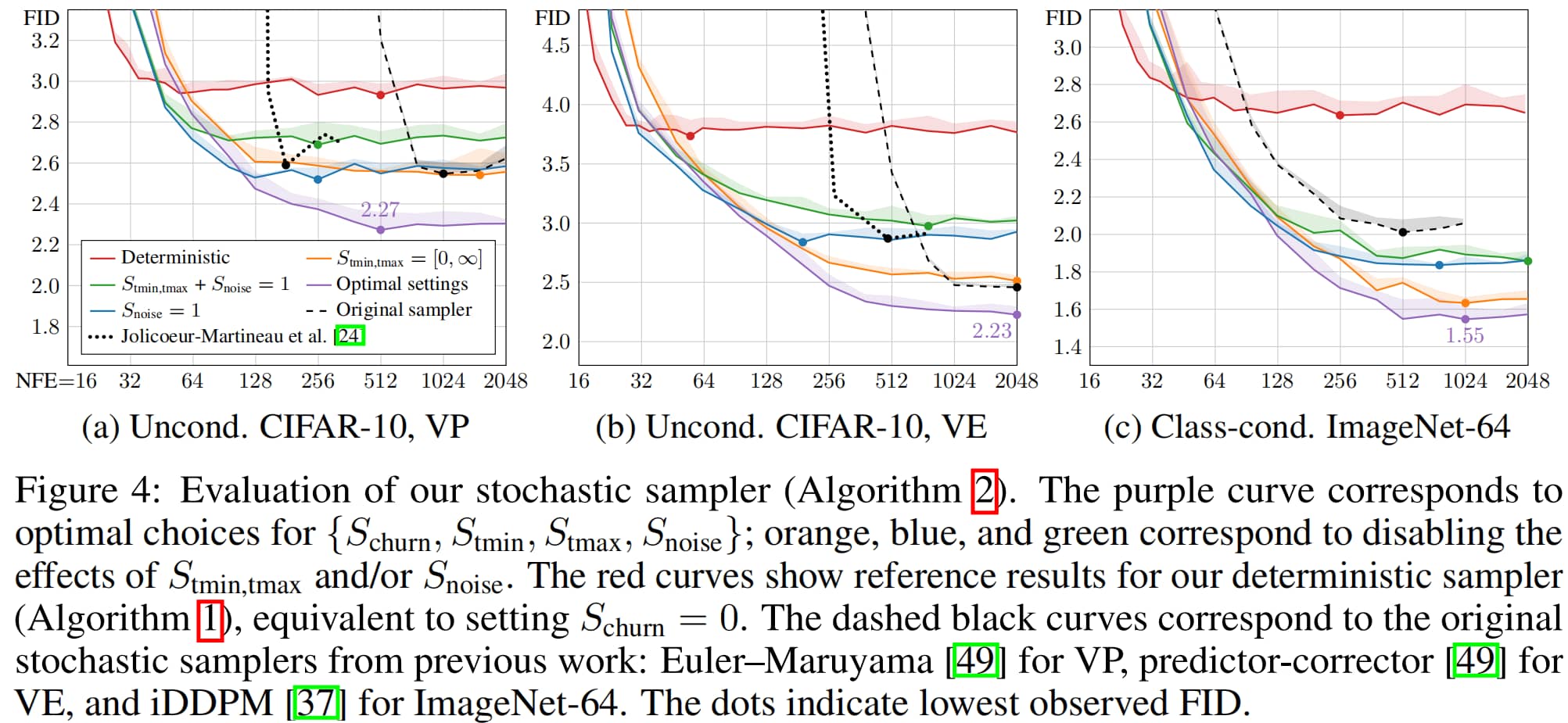
图4显示，本文提出的随机采样器显著优于以往的采样器[24,37,49]，尤其是在步数较少的情况下。Jolicoeur-Martineau等人[24]采用了标准的高阶自适应SDE求解器[41]，该求解器的性能可作为此类自适应求解器的通用基准。本文的采样器则针对具体应用场景进行了定制（例如，将噪声注入与ODE步序贯执行），且并非自适应求解器。目前尚未有定论的是：在扩散模型采样中，自适应求解器是否能比参数调优后的固定调度方案带来净收益。

仅通过改进采样器，我们就将原本FID（弗雷歇初始距离）为2.07的ImageNet-64模型[9]，优化至FID 1.55，该结果已非常接近当前最先进（SOTA）水平；此前，级联扩散模型[17]的FID为1.48（注：原文此处内容未完整呈现，暂译至此）。

此前，级联扩散模型（cascaded diffusion）[17]的FID为1.48，无分类器引导（classifier-free guidance）[18]的FID为1.55，StyleGAN-XL[45]的FID为1.52。虽然我们的结果展示了通过改进采样器可实现的潜在收益，但也凸显了随机性的主要缺陷：若要获得最佳结果，必须做出多项依赖特定模型的启发式选择（无论这些选择是隐式还是显式的）。事实上，我们不得不通过网格搜索，逐案例确定 $\{S_{churn}, S_{tmin}, S_{tmax}, S_{noise}\}$ 的最优值（详见附录E.2）。这引发了一个普遍性担忧：若将随机采样作为评估模型改进效果的主要手段，可能会在不经意间影响与模型架构和训练相关的设计选择。

---

预处理与训练

回顾

DDPM/DDIM/VP

损失函数

$$\mathcal{L}_{\text{VP}} = \mathbb{E}_{\boldsymbol{x}_t, \boldsymbol{\varepsilon} \sim \mathcal{N}(0, \mathbf{I})} \lambda(t) \left\| \boldsymbol{\varepsilon}_\theta(\boldsymbol{x}_t; t) - \boldsymbol{\varepsilon} \right\|_2^2$$

其中，$\boldsymbol{\varepsilon}$ 表示真实噪声，$\boldsymbol{\varepsilon} \sim \mathcal{N}(0, \mathbf{I})$，$\boldsymbol{\varepsilon}_\theta$ 表示神经网络预测的噪声。

带入EDM框架的去噪模型 $D_\theta(\boldsymbol{x}; \sigma)$（输入为加噪图像 $\boldsymbol{x}_t$，输出为原图像 $\boldsymbol{x}_0$）

DDPM的一步加噪公式：

$$\boldsymbol{x}_t = \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\varepsilon}$$

可变形为，

$$\boldsymbol{x}_0 = \frac{\boldsymbol{x}_t - \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\varepsilon}}{\sqrt{\bar{\alpha}_t}}$$

套用DDPM加噪公式，去噪器 $D_\theta$ 变为，

$$D_\theta(\boldsymbol{x}_t; \sigma(t)) \approx \boldsymbol{x}_0 \approx \frac{\boldsymbol{x}_t - \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\varepsilon}}{\sqrt{\bar{\alpha}_t}} \approx \frac{1}{\sqrt{\bar{\alpha}_t}} \boldsymbol{x}_t - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}} \boldsymbol{\varepsilon}_\theta(\boldsymbol{x}_t; t)$$

SMLD/VE

损失函数为：

$$\mathcal{L}_{\text{SM}} = \mathbb{E}_{\boldsymbol{x}, \sigma \sim \mathcal{N}(0, \mathbf{I})} \lambda(\sigma) \left\| s_\theta(\boldsymbol{x}; \sigma) - \nabla_{\boldsymbol{x}} \log p(\boldsymbol{x}; \sigma) \right\|_2^2$$

同样，$\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x}; \sigma)$ 表示真实分数，$s_\theta$ 表示神经网络预测的分数。

按上文中 $D_\theta$ 的表达式，

$$\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x}; \sigma) \approx \frac{D_\theta(\boldsymbol{x}; \sigma) - \boldsymbol{x}}{\sigma^2}$$

整理成 $D_\theta$ 在等式左边，有：

$$D_\theta(\boldsymbol{x}; \sigma) \approx \boldsymbol{x} + \sigma^2 \nabla_{\boldsymbol{x}} \log p(\boldsymbol{x}; \sigma) \approx \boldsymbol{x} + \sigma^2 s_\theta(\boldsymbol{x}; \sigma)$$

Flow Matching

损失函数为：

$$\mathcal{L}_{\text{FM}} = \mathbb{E}_{\boldsymbol{x}_t, t, \boldsymbol{\varepsilon} \sim \mathcal{N}(0, \mathbf{I})} \lambda(t) \left\| v_\theta(\boldsymbol{x}_t; t) - (\boldsymbol{x}_0 - \boldsymbol{\varepsilon}) \right\|_2^2$$

其中，$\boldsymbol{x}_0$ 为纯净原始图像，$\boldsymbol{\varepsilon} \sim \mathcal{N}(0, \mathbf{I})$。

因为 $D_\theta(\boldsymbol{x}; \sigma) \approx \boldsymbol{x}_0$ ，有

$$v_\theta(\boldsymbol{x}_t; t) \approx D_\theta(\boldsymbol{x}_t; \sigma(t)) - \boldsymbol{\varepsilon}$$

Flow Matching 加噪公式：

$$\boldsymbol{x}_t = (1 - t)\boldsymbol{x}_0 + t\boldsymbol{\varepsilon}$$

由 Flow Matching 加噪公式，可得：

$$\boldsymbol{\varepsilon} = \frac{\boldsymbol{x}_t - (1 - t)\boldsymbol{x}_0}{t} \approx \frac{\boldsymbol{x}_t - (1 - t)D_\theta(\boldsymbol{x}_t; \sigma(t))}{t}$$

代回，

$$\begin{align*} v_\theta(\boldsymbol{x}_t; t) &\approx D_\theta(\boldsymbol{x}_t; \sigma(t)) - \boldsymbol{\varepsilon} \\ &= D_\theta(\boldsymbol{x}_t; \sigma(t)) - \frac{\boldsymbol{x}_t - (1 - t)D_\theta(\boldsymbol{x}_t; \sigma(t))}{t} \\ &= \frac{1}{t} D_\theta(\boldsymbol{x}_t; \sigma(t)) - \frac{1}{t} \boldsymbol{x}_t \end{align*}$$

把 $D_\theta$ 写到等式的左边，有：

$$D_\theta(\boldsymbol{x}_t; \sigma(t)) \approx \boldsymbol{x}_t + t\,v_\theta(\boldsymbol{x}_t; t)$$

大一统训练模型

Q：为什么要加入多个前处理和后处理操作？

A：为了使 $D_\theta$ 能够稳定训练，也即 $\mathcal{L}$ 保持稳定，不能因为各参数设置而变化过快。

两种选择：

1. 在目标附近采用更短的步长；
2. 扭曲噪声调度，以在目标附近花费更多时间。

信号尺度问题

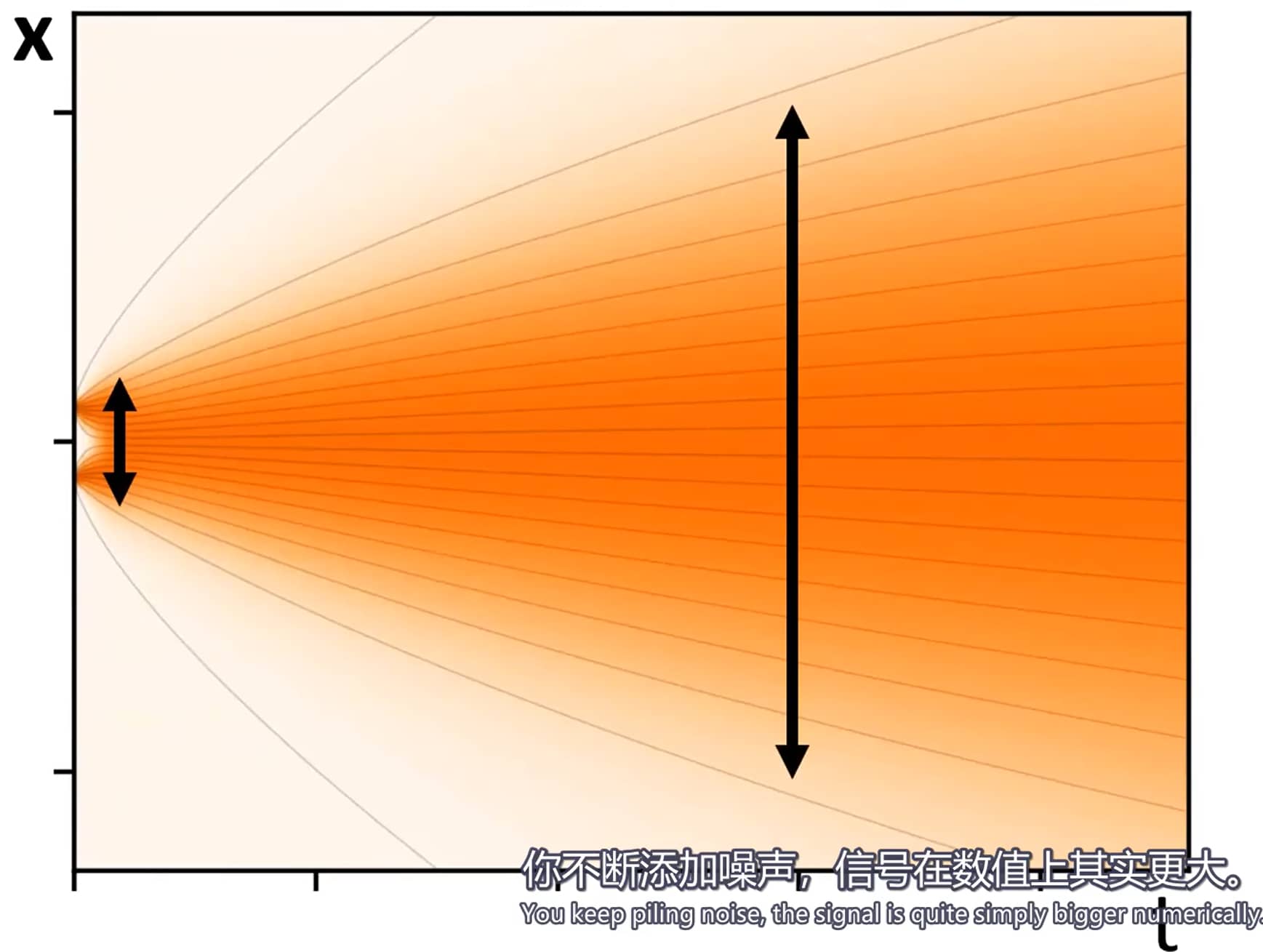
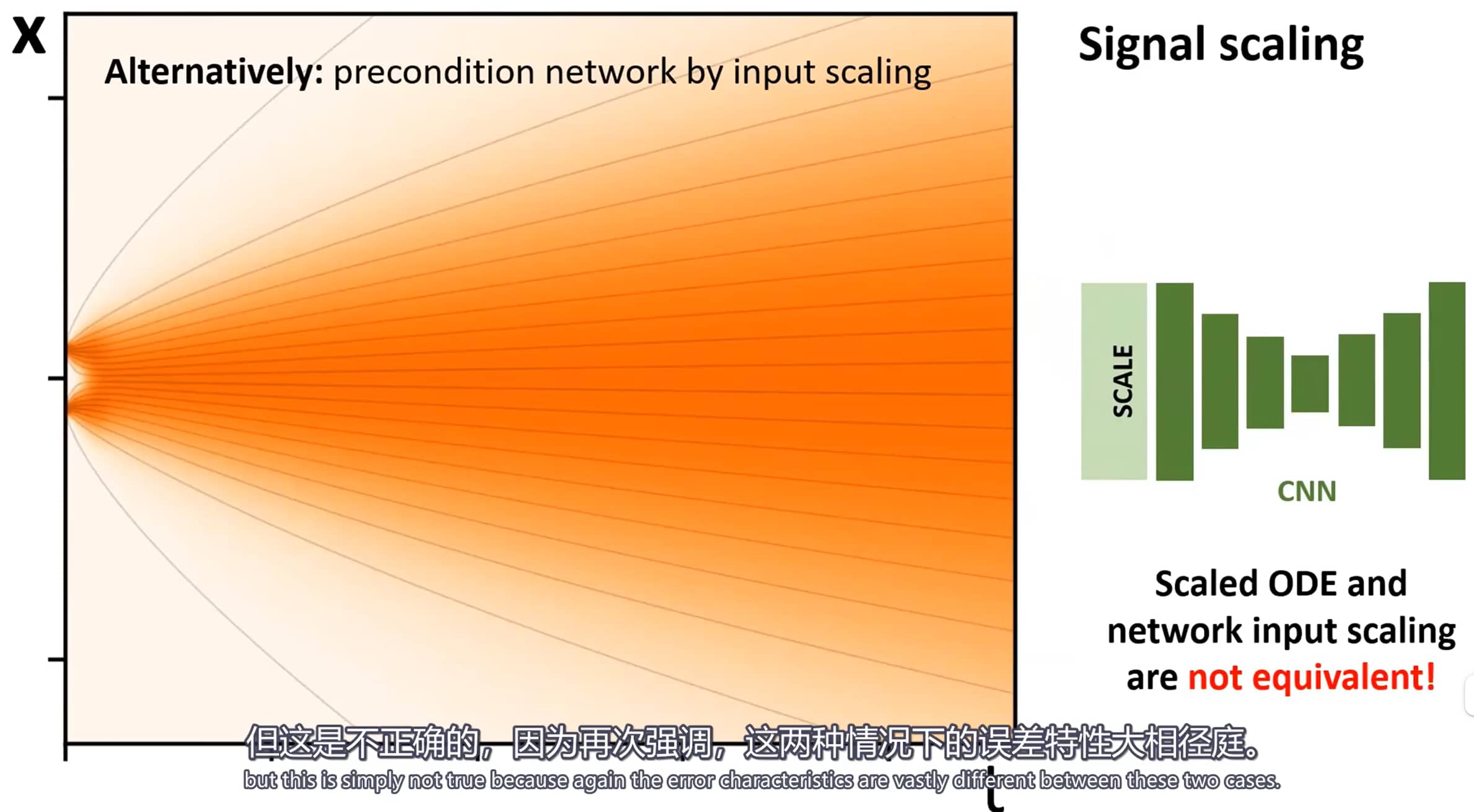
信号尺度差异过大会导致神经网络难以训练

===========================

在有监督训练神经网络的领域，存在多种已知的良好实践。例如，建议将输入和输出信号的幅度固定为特定值（如单位方差），并避免单样本梯度幅度出现大幅波动。

直接训练神经网络对去噪器 $D$ 进行建模的方案远非理想——例如，输入 $\boldsymbol{x} = \boldsymbol{y} + \boldsymbol{n}$ 是干净信号 $\boldsymbol{y}$ 与噪声 $\boldsymbol{n}$（$\boldsymbol{n} \sim \mathcal{N}(0, \sigma^2 \boldsymbol{I})$）的叠加，其幅度会随噪声水平 $\sigma$ 发生极大变化。

因此，常规做法是不将 $D_\theta$ 直接表示为神经网络，而是训练另一个网络 $F_\theta$，再由 $F_\theta$ 推导得到 $D_\theta$。

对比上面三式，可以总结出如下通式，

借鉴此前“自适应混合信号与噪声”的参数化思路，我们提出为神经网络添加与 $\sigma$ 相关的跳连（连接），以实现预处理——该跳连使网络可灵活估计干净信号 $\boldsymbol{y}$、噪声 $\boldsymbol{n}$，或二者之间的中间状态。据此，我们将 $D_\theta$ 表示为以下形式：

$$D_\theta(x;\sigma) = c_{skip}(\sigma)x + c_{out}(\sigma)F_\theta\left(c_{in}(\sigma)x; c_{noise}(\sigma)\right) \tag{6}$$

其中，

• $F_\theta$ 是待训练的神经网络；
• $c_{skip}(\sigma)$ 用于调节跳连强度；
• $c_{in}(\sigma)$ 和 $c_{out}(\sigma)$ 分别对输入和输出幅度进行缩放；
• $c_{noise}(\sigma)$ 将噪声水平 $\sigma$ 映射为 $F_\theta$ 的条件输入。

注1：$c_{in}$ 用于进行信号放缩。

例如，DDPM/DDIM 中 $s(t) = \sqrt{\bar{\alpha}_t}$，$c_{in}(\sigma) = \sqrt{\bar{\alpha}(\sigma^{-1}(\sigma))}$；SMLD 中 $s(t) = 1$，$c_{in}(\sigma) = 1$；Flow Matching 中 $s(t) = 1 - t$，$c_{in}(\sigma) = 1 - t = 1 - \sigma^{-1}(\sigma)$

注2：$c_{noise}(\sigma)$ 是一个对 $\sigma$ 进行变换的函数，其目的是让另一个条件输入与标准化的 $x$ 相适应。

例如，在 DDPM/DDIM 的 $\varepsilon_\theta (x_t,t)$ 中，其对应的 $c_{noise}$ 就是 $t$（时间编码），可以视作是 $c_{noise} = \sigma^{-1}(\sigma(t)) = t$；而在 SMLD 中，$c_{noise}$ 则为 $c_{noise} = \log (\frac{1}{2} \sigma)$

$c_{noise} = \sigma^{-1}(\sigma(t)) = t$（DDPM/DDIM）

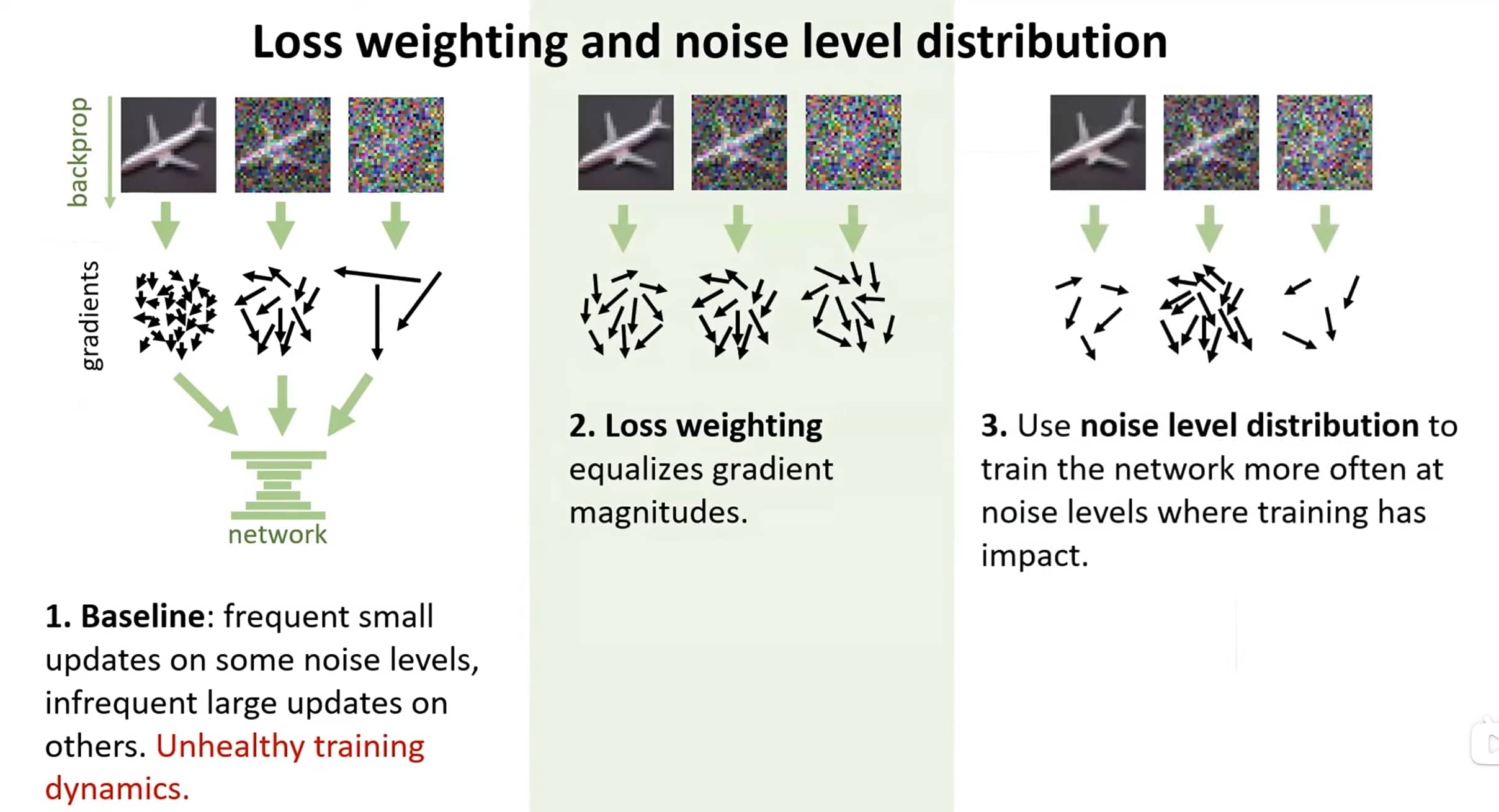
损失加权

对式（2）在所有噪声水平上取加权期望，可得到整体训练损失：$\mathbb{E}_{\sigma,y,n}\left[\lambda(\sigma)\|D(y+n;\sigma) - y\|_2^2\right]$，其中 $\sigma \sim p_{train}$（噪声水平服从训练采样分布）、$y \sim p_{data}$（干净数据服从数据分布）、$n \sim \mathcal{N}(0,\sigma^2I)$（噪声服从高斯分布）。采样特定噪声水平 $\sigma$ 的概率由 $p_{train}(\sigma)$ 决定，对应的权重由 $\lambda(\sigma)$ 决定。

既然 $D_\theta(\boldsymbol{x};\sigma)$ 是一个单纯的去噪模型，那它的损失函数也必定是一个单纯的与噪声的距离度量，假设就是MSE损失函数形式:

$$\begin{align*} \mathcal{L}_{\text{diff}} &= \mathbb{E}_{\sigma \sim p_{\text{train}},\boldsymbol{x},\boldsymbol{y} \sim p_{\text{data}}} \left[ \lambda(\sigma) \| D_\theta(\boldsymbol{x}; \sigma) - \boldsymbol{y} \|_2^2 \right] \\ &= \mathbb{E}_{\sigma \sim p_{\text{train}},\boldsymbol{y} \sim p_{\text{data}}, \boldsymbol{n} \sim \mathcal{N}(0, \sigma^2 \mathbf{I})} \left[ \lambda(\sigma) \| D_\theta(\boldsymbol{y} + \boldsymbol{n}; \sigma) - \boldsymbol{y} \|_2^2 \right] \end{align*}$$

$p_{\text{train}}$是$\sigma$的分布，也即在训练的时候，每个噪声水平（时间点）不一定是服从均匀分布。

结合式 <a href="#eq:6">(6)</a>，我们可将该损失用网络 $F_\theta$ 的原始输出等价表示为：

$$\begin{align*} \mathcal{L}_\text{diff} &= \mathbb{E}_{\sigma,\boldsymbol{y},\boldsymbol{n}} \left[ \lambda(\sigma) \left\| c_{\text{skip}}(\sigma)(\boldsymbol{y}+\boldsymbol{n}) + c_{\text{out}}(\sigma) F_\theta\left( c_{\text{in}}(\sigma)(\boldsymbol{y}+\boldsymbol{n}); c_{\text{noise}}(\sigma) \right) - \boldsymbol{y} \right\|_2^2 \right] \\ &= \mathbb{E}_{\sigma,\boldsymbol{y},\boldsymbol{n}}\left[ \underbrace{\lambda(\sigma)c_{out}(\sigma)^2}_{\text{有效权重}} \left\| \underbrace{F_\theta\left(c_{in}(\sigma)\cdot(\boldsymbol{y}+\boldsymbol{n}); c_{noise}(\sigma)\right)}_{\text{网络输出}} - \underbrace{\frac{1}{c_{out}(\sigma)}\left(\boldsymbol{y} - c_{skip}(\sigma)\cdot(\boldsymbol{y}+\boldsymbol{n})\right)}_{\text{有效训练目标}} \right\|_2^2 \right] \tag{7} \end{align*}$$

超参数的选取

要使得训练稳定，不能使得噪声不同的时候，损失函数产生大幅度的变化，因此EDM考虑了以下四点来设计 $c_{\text{in}}(\sigma)$、$c_{\text{out}}(\sigma)$、$c_{\text{skip}}(\sigma)$、$\lambda(\sigma)$：

此处没有提到 $c_{noise}$，是因为它已经蕴含在网络设计里面了（设计条件输入时，就已经规定好了）

超参数选取主要遵循以下原则：

1. 神经网络的输入保持单位方差，规范了 $c_{\text{in}}(\sigma)$；
2. 训练目标保持单位方差，规范了 $c_{\text{out}}(\sigma)$ 和 $c_{\text{skip}}(\sigma)$；
3. 等价对待所有的噪声水平损失函数，规范了 $\lambda(\sigma)$；

对 $c_{\text{in}}(\sigma)$ 的限制

$$\mathbb{D}_{\boldsymbol{y},\boldsymbol{n}} \left[ c_{\text{in}}(\sigma)(\boldsymbol{y} + \boldsymbol{n}) \right] = 1 \Rightarrow c_{\text{in}}(\sigma) = \frac{1}{\sigma^2 + \sigma_{\text{data}}^2}$$

对 $c_{\text{out}}(\sigma), c_{\text{skip}}(\sigma)$ 的限制

$$\mathbb{D}_{\boldsymbol{y},\boldsymbol{n}} \left[ \frac{1}{c_{\text{out}}(\sigma)} \left( \boldsymbol{y} - c_{\text{skip}}(\sigma)(\boldsymbol{y} + \boldsymbol{n}) \right) \right] = 1 \Rightarrow c_{\text{out}}^2(\sigma) = \left( 1 - c_{\text{skip}}(\sigma) \right)^2 \sigma_{\text{data}}^2 + c_{\text{skip}}^2(\sigma) \sigma^2$$

可以发现上式的 $c_{\text{out}}(\sigma)$ 和 $c_{\text{skip}}(\sigma)$ 相关，还需要进行解耦。因为 $c_{\text{out}}(\sigma)$ 直接关系到神经网络 $F_\theta$ 的输出尺度，太大的 $c_{\text{out}}(\sigma)$ 会放大 $F_\theta$ 的估计误差，故 EDM 通过求解下面的最优化问题来先求出 $c_{\text{skip}}(\sigma)$ 的值：

$$c_{\text{skip}}(\sigma) = \arg\min_{c_{\text{skip}}(\sigma)} c_{\text{out}}^2(\sigma)$$

这是一个凸优化问题，令其导数为0，

$$\frac{\mathrm{d}c_{\text{out}}^2(\sigma)}{\mathrm{d}\sigma} = 0$$

经过运算可得，

$$c_{\text{skip}}(\sigma) = \frac{\sigma_{\text{data}}^2}{\sigma^2 + \sigma_{\text{data}}^2}$$

代回，得到，

$$c_{\text{out}}(\sigma) = \frac{\sigma \cdot \sigma_{\text{data}}}{\sqrt{\sigma^2 + \sigma_{\text{data}}^2}}$$

对 $\lambda(\sigma)$ 的限制

令 $w(\sigma) = 1$，也即

$$\lambda(\sigma) C_{\text{out}}^2(\sigma) = 1 \Rightarrow \lambda(\sigma) = \frac{\sigma^2 + \sigma_{\text{data}}^2}{\left( \sigma \cdot \sigma_{\text{data}} \right)^2}$$

$$\lambda(\sigma) = \frac{1}{c_{\text{out}}^2(\sigma)}$$

该形式清晰呈现了 $F_\theta$ 的有效训练目标，使我们能够基于基本原理确定预处理函数的合适选择。如附录B.6所述，我们推导得到的（预处理函数）选择方案（注：原文此处内容未完整呈现，暂译至此）。

我们在表1中列出的（预处理函数）选择方案，是通过以下要求推导得到的：网络输入和训练目标需具有单位方差（由 $c_{in}$、$c_{out}$ 实现），且对 $F_\theta$ 的误差放大效应尽可能小（由 $c_{skip}$ 实现）。而 $c_{noise}$ 的公式则是通过实验确定的。

表2展示了一系列训练配置的弗雷歇初始距离（FID），所有结果均使用第3节提出的确定性采样器评估。我们以Song等人[49]提出的基准训练配置为起点，该配置在方差保持（VP）和方差爆炸（VE）两种场景下差异显著，因此我们分别提供了两种场景的结果（对应配置A）。为了获得更具意义的对比基准，我们重新调整了基础超参数（对应配置B），并通过移除最低分辨率层、同时将最高分辨率层的容量翻倍，提升了模型的表达能力（对应配置C）；更多细节详见附录F.3。随后，我们将 $\{c_{in}、c_{out}、c_{noise}、c_{skip}\}$ 的原始选择替换为本文提出的预处理方案（对应配置D），结果基本保持不变——但方差爆炸（VE）模型在64×64分辨率下的性能得到了显著提升。需要说明的是，我们提出的预处理方案并非直接提升FID，其主要优势在于增强了训练的鲁棒性，使我们能够专注于重新设计损失函数，且不会产生负面影响。

=========================

式（8）表明，按照式（7）的预处理方式训练
$F_\theta$ 时，产生的每样本有效损失权重为 $\lambda(\sigma)c_{out}(\sigma)^2$。为平衡有效损失权重，我们令 $\lambda(\sigma) = 1/c_{out}(\sigma)^2$，这一设置还能使整个 $\sigma$ 范围内的初始训练损失趋于均衡，如图5a中的绿色曲线所示。

最后，我们需要确定训练时的噪声采样分布 $p_{train}(\sigma)$，即训练过程中如何选择噪声水平。观察训练后各 $\sigma$ 对应的损失（蓝色和橙色曲线）可发现：只有在中等噪声水平下，损失才有可能显著降低；在极低噪声水平下，识别微乎其微的噪声成分既困难又无实际意义；而在极高噪声水平下，训练目标与趋近于数据集均值的正确结果始终存在较大差异。因此，我们将 $p_{train}(\sigma)$ 设置为简单的对数正态分布，使训练聚焦于上述相关噪声范围，具体参数详见表1，分布示意图如图5a中的红色曲线所示。

表2显示，当我们提出的 $p_{train}$ 和 $\lambda$（对应配置E）与预处理方案（配置D）结合使用时，所有场景下的FID均得到显著提升。在同期研究中，Choi等人[6]提出了一种类似方案，优先选择与“形成感知上可识别的图像内容”最相关的噪声水平。但他们仅单独考虑了 $\lambda$ 的选择，因此整体改进效果较弱。

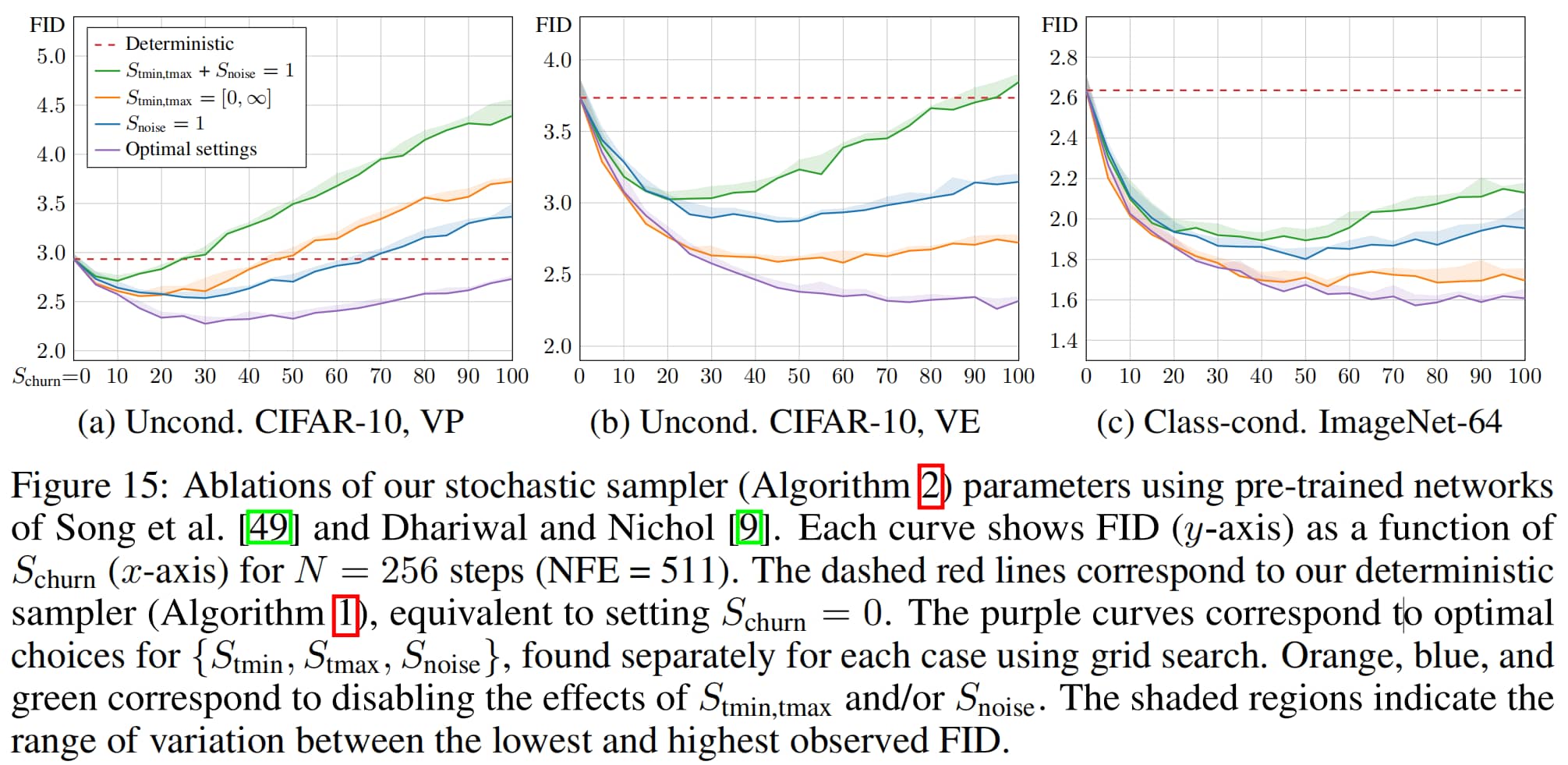
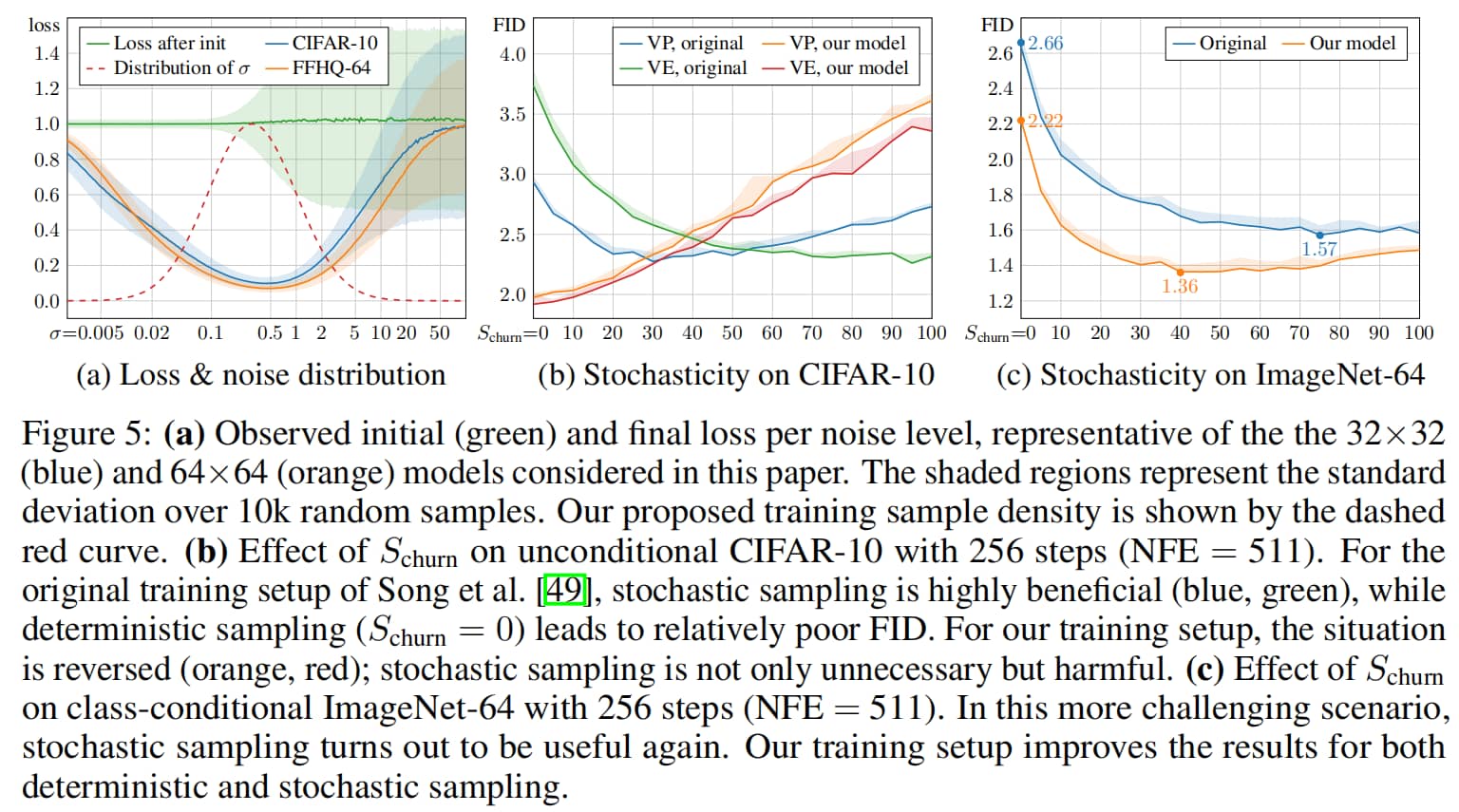
图5：(a) 观测到的初始（绿色）与最终损失随噪声水平变化曲线，分别代表本文研究的32×32（蓝色）和64×64（橙色）模型。阴影区域表示10,000次采样样本的标准差。我们提出的训练样本密度由红色虚线曲线表示。(b) churn参数在256步采样（NFE=511）下对无条件CIFAR-10数据集的影响。在Song等人[49]原始训练配置中，随机采样（蓝色、绿色）效果显著优于确定性采样（churn=0），后者导致相对较差的FID指标。而采用我们的训练配置时（橙色、红色），情况发生逆转——随机采样不仅不必要反而有害。(c) churn参数在256步采样（NFE=511）下对类别条件ImageNet-64数据集的影响。在这个更具挑战性的场景中，随机采样再次展现出优势。我们的训练配置同时提升了确定性采样和随机采样的效果。

$\sigma$ 的选取

EDM 设计 $p_{train}(\sigma)$ 为如下形式，

$$\ln (\sigma) \sim \mathcal{N}(P_{\text{mean}}, P_{\text{std}}^2), \quad P_{\text{mean}} = -1.2, \ P_{\text{std}} = 1.2$$

采用上述分布的原因：

1. 根据实验结果，损失函数下降比较多的地方是中等噪声水平；
2. 当噪声水平较低时，模型预测的相对误差较大，损失函数难以下降；
3. 当噪声水平较高时，对真实图像扰动较大，每一个样本的学习目标与样本均值目标差距较大，损失函数也难以下降。

于是，EDM 选择让网络侧重于在中等噪声水平下学习。如上图（a）

增强正则化

为防止小规模数据集训练扩散模型时常见的过拟合问题，我们借鉴了生成对抗网络（GAN）领域的增强流程[25]。该流程包含多种几何变换（详见附录F.2），我们在向训练图像添加噪声前对其应用这些变换。为防止增强操作“泄露”到生成图像中，我们将增强参数作为条件输入传入 $F_\theta$；在推理阶段，我们将这些参数设为0，以确保生成的图像均未经过增强处理。

表2显示，数据增强能带来一致性的性能提升（对应配置F）：在类别条件和无条件CIFAR-10任务上，模型分别取得了1.79和1.97的新最先进（SOTA）FID，超过了此前1.85[45]和2.10[53]的记录。

随机采样再探讨

有趣的是，如图5b、c所示，随着模型本身性能的提升，随机采样的必要性似乎在降低。在CIFAR-10数据集上使用我们的训练配置时（图5b），确定性采样能取得最佳结果，而任何程度的随机采样都会产生不利影响。

ImageNet-64实验

作为最后一项实验，我们基于提出的训练改进方案，从零开始训练了一个类别条件ImageNet-64模型。该模型取得了新的最先进（SOTA）FID，数值为1.36，而此前的纪录为1.48[17]。我们采用了ADM架构[9]且未做任何修改，同时使用我们的E配置进行训练，并仅做了少量调优；详细细节参见附录F.3。我们发现过拟合问题无需担忧，因此未采用增强正则化。如图5c所示，随机采样的最优强度远低于预训练模型的情况，但与CIFAR-10数据集不同，随机采样的效果明显优于确定性采样。这表明，对于多样性更高的数据集，随机采样仍能持续带来收益。

留着

轨迹曲率与噪声调度

ODE解轨迹的形状由函数 $\sigma(t)$ 和 $s(t)$ 定义。选择这两个函数是降低上述截断误差的一种途径，因为截断误差的大小可认为与 $\frac{dx}{dt}$ 的曲率成比例。

我们认为，这两个函数的最优选择是 $\sigma(t) = t$ 且 $s(t) = 1$，这也是DDIM[47]所采用的选择。在此选择下，式（4）所示的ODE可简化为 $\frac{dx}{dt} = \frac{x - D(x;t)}{t}$，且 $\sigma$ 与 $t$ 变得可互换。

这一选择带来的直接结果是：在任意 $x$ 和 $t$ 下，只需向 $t=0$ 执行一步欧拉法，即可得到去噪图像 $D_\theta(x;t)$。因此，解轨迹的切线始终指向去噪器的输出。可以预期，该切线随噪声水平的变化会非常平缓，这对应于大致线性的解轨迹。图3c中的一维ODE示意图印证了这一直观认知：在噪声水平极大和极小的区域，解轨迹均接近线性，仅在中间一个小区域内存在明显曲率。这种效应在真实数据上同样可见（图1b）：不同去噪器目标之间的变化仅发生在一个相对狭窄的 $\sigma$ 范围内。在我们所倡导的调度方案下，这意味着ODE的高曲率区域被限制在同一范围内。

将 $\sigma(t) = t$ 且 $s(t) = 1$ 的实验结果以图2中的红色曲线展示。由于DDIM已采用相同的选择，因此在ImageNet-64数据集上，红色曲线与绿色曲线完全重合。然而，VP（方差保持）和VE（方差爆炸）模型从“脱离原始调度方案”中获得了显著收益。

讨论

本节中为改进确定性采样所做的各项选择，已汇总至表1的“采样（Sampling）”部分。这些选择共同作用，大幅降低了生成高质量结果所需的神经函数评估次数（NFE）：方差保持（VP）模型降低7.3倍，方差爆炸（VE）模型降低300倍，去噪扩散隐式模型（DDIM）降低3.2倍，对应图2中突出显示的NFE数值。在实际应用中，在单张NVIDIA V100显卡上，每秒可生成26.3张高质量的CIFAR-10图像。

这种一致性的改进验证了我们的假设：采样过程与各模型的原始训练方式相互正交（即彼此独立，互不影响）。为进一步验证，我们将自适应RK45方法[11]结合本文提出的调度方案进行实验，结果以图2中的黑色虚线展示；该复杂常微分方程（ODE）求解器的计算成本远超其带来的收益，因此并非最优选择。

6 结论

我们将扩散模型纳入统一框架的方法，呈现出了模块化的设计结构。这使得我们能够针对性研究各个组件，进而有可能更好地覆盖可行设计空间。在我们的测试中，这种设计使我们能够直接替换各类早期模型中的采样器，从而显著提升结果性能。例如，在ImageNet-64数据集上，我们的采样器将一个普通模型（FID为2.07）转变为能与此前最先进（SOTA）模型（FID为1.48[17]）竞争的模型；而结合训练改进后，模型更是取得了1.36的SOTA FID。在CIFAR-10数据集上，我们仅需35次模型评估、采用确定性采样并使用小型网络，就取得了新的最先进结果。

当前的高分辨率扩散模型要么依赖独立的超分辨率步骤[17,36,40]、子空间投影[23]、超大网络[9,49]，要么采用混合方法[39,42,53]——我们认为，我们的研究贡献与这些扩展方向相互正交。尽管如此，对于更高分辨率的数据集，我们的许多参数值可能仍需重新调整。此外，我们认为，随机采样与训练目标之间的精确相互作用，仍是未来值得研究的有趣问题。

预处理与训练

回顾两个误差来源：

• 采样中的离散化步骤

  • 我们已通过预训练网络研究了这一点

• **不准确的神经去噪器（又名得分函数）**接下来的工作：

  • 改进网络预处理（例如，输入和输出缩放）
  • 改进训练（损失缩放，以及在哪些噪声水平上训练？）

• 我们不会（大幅）改变层架构等。

Preconditioning

• 为了让CNN更易处理：

  • (A) 始终向网络输入 单位标准差的输入（unit stdev inputs）
  • (B) ……并使用 单位标准差的目标（unit stdev targets）进行训练

• 网络会产生误差。我们应当：

  • © 最小化网络对去噪器输出的贡献

• 我们的噪声水平变化极大，因此这一点至关重要！

• 扩散模型的模块化设计

  • 训练、采样与网络架构并非紧密耦合

• 精心设计每个“模块”可带来显著改进

• 随机性是把双刃剑

• 更高分辨率、网络架构、条件设定/引导、大规模数据集……？

  • 已成熟到可对基础理论开展系统性分析

改进Heun步

算法2