EDM：扩散模型的设计空间

2025/08/04 - 至今
待完善

主要参考资料

本篇文章主要基于《Elucidating the Design Space of Diffusion-Based
Generative Models》以及以下几个视频、博文。

数学推导参考：B站讲解 Double童发发 - EDM论文讲解之扩散模型通用框架系列、苏剑林-科学空间-一般框架之SDE篇

整体脉络、相关图片参考：B站讲座 -【双语】NVIDIA - EDM 以及 论文相关博文

本文按照上述讲座顺序，分为四个部分：

• 第一部分：通用框架
  • 识别现有研究中的可变部分
• 第二部分：确定性采样
  • 高效求解 ODE
• 第三部分：随机采样
  • 为什么用 SDE？如何进行随机步长计算？
• 第四部分：预处理与训练
  • 如何训练用于评估单步的卷积神经网络（CNN）？

通用框架

通过连续时间随机过程将数据扰动至纯噪声

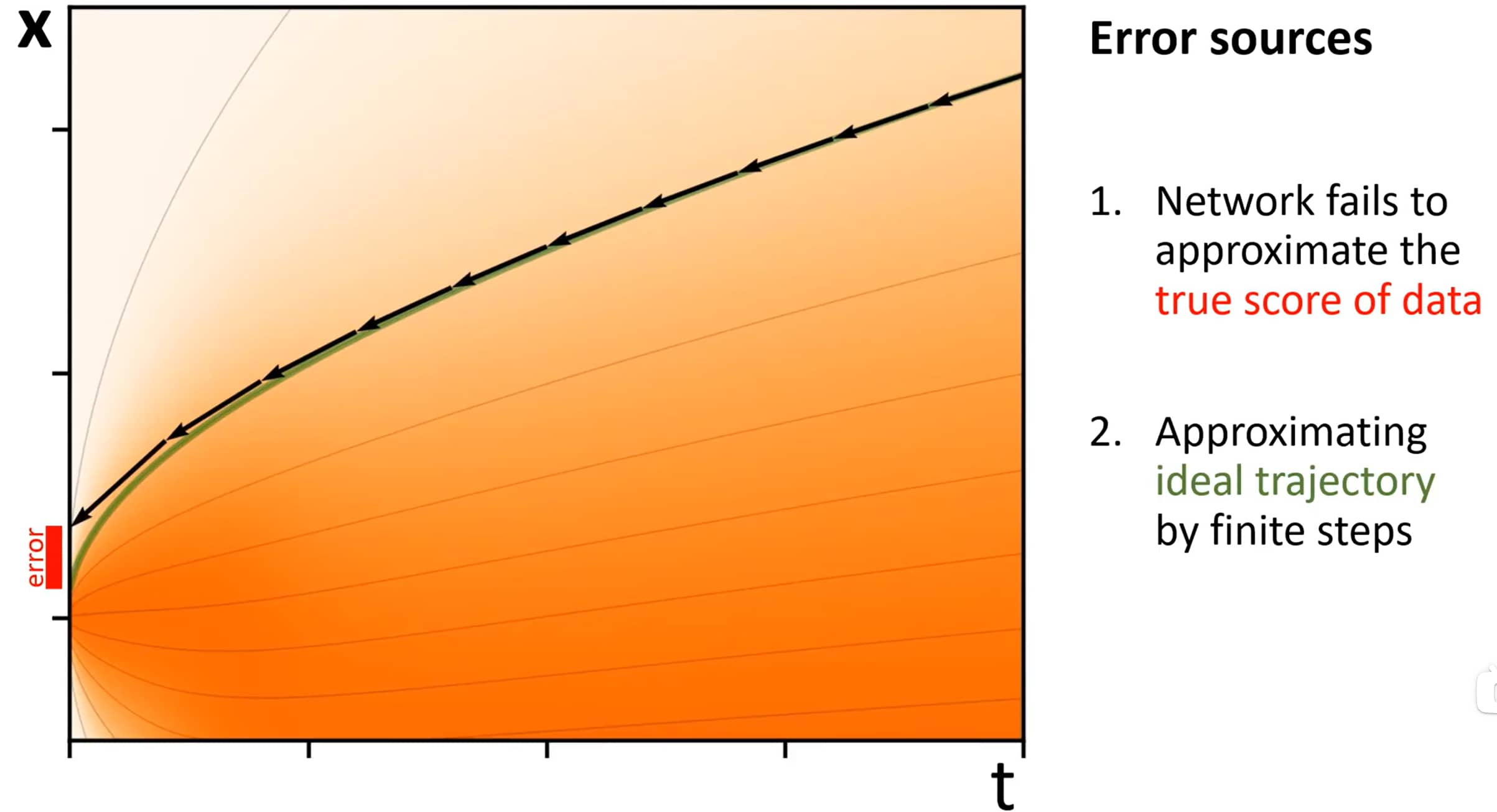SDE视角下，扩散模型出现的两个问题

1. 网络无法逼近数据的 真实得分：这导致采样轨迹朝着错误方向演进。上图当前轨迹（黑色）为错误采样链，在左侧与目标之间存在error；
2. 通过有限步长逼近 理想轨迹：为了近似绿色轨迹，如果每步太长，则会显著偏离目标轨迹；如果每步太短，则会消耗过多计算资源。

事实上，以上两点分别对应于 Traning过程 和 Sampling过程。

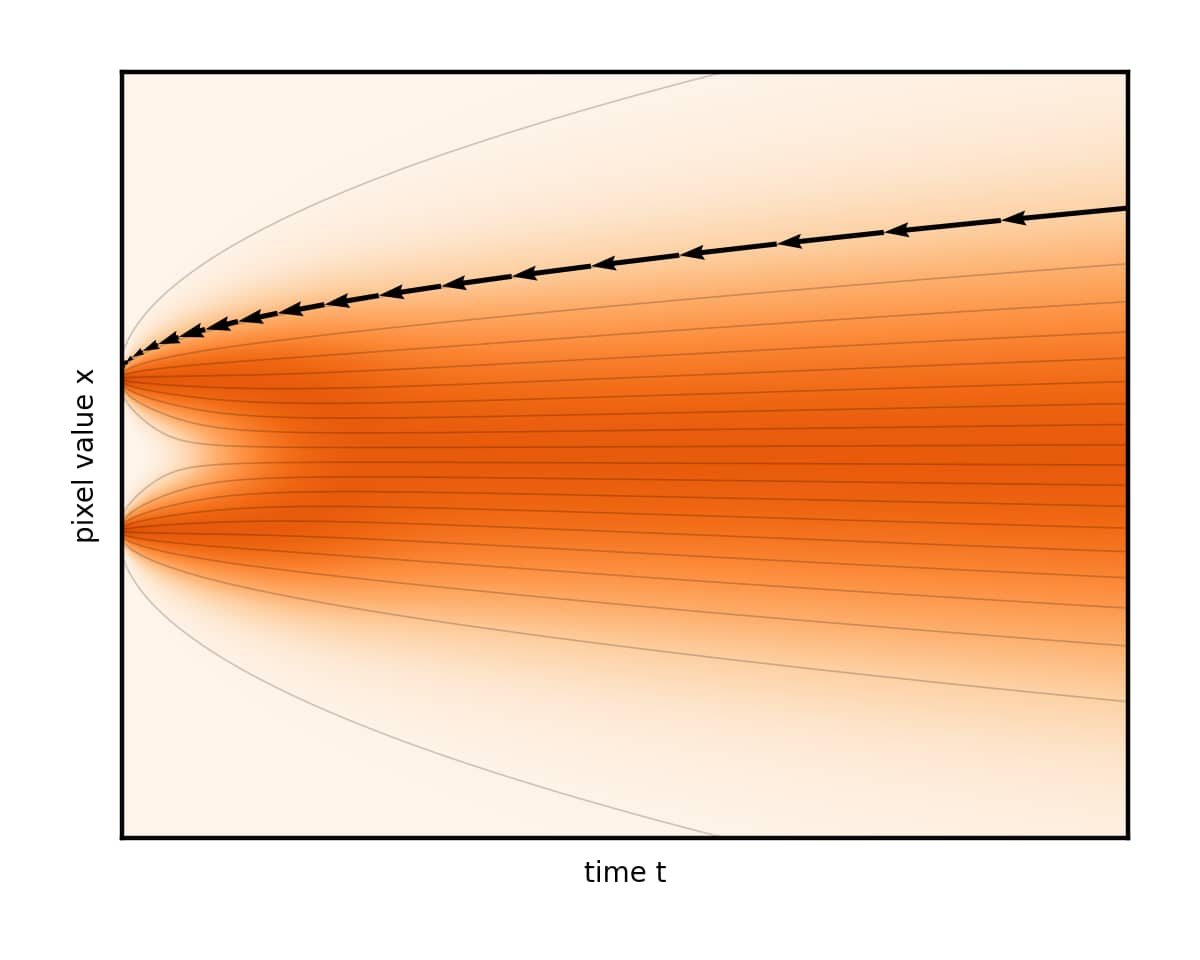
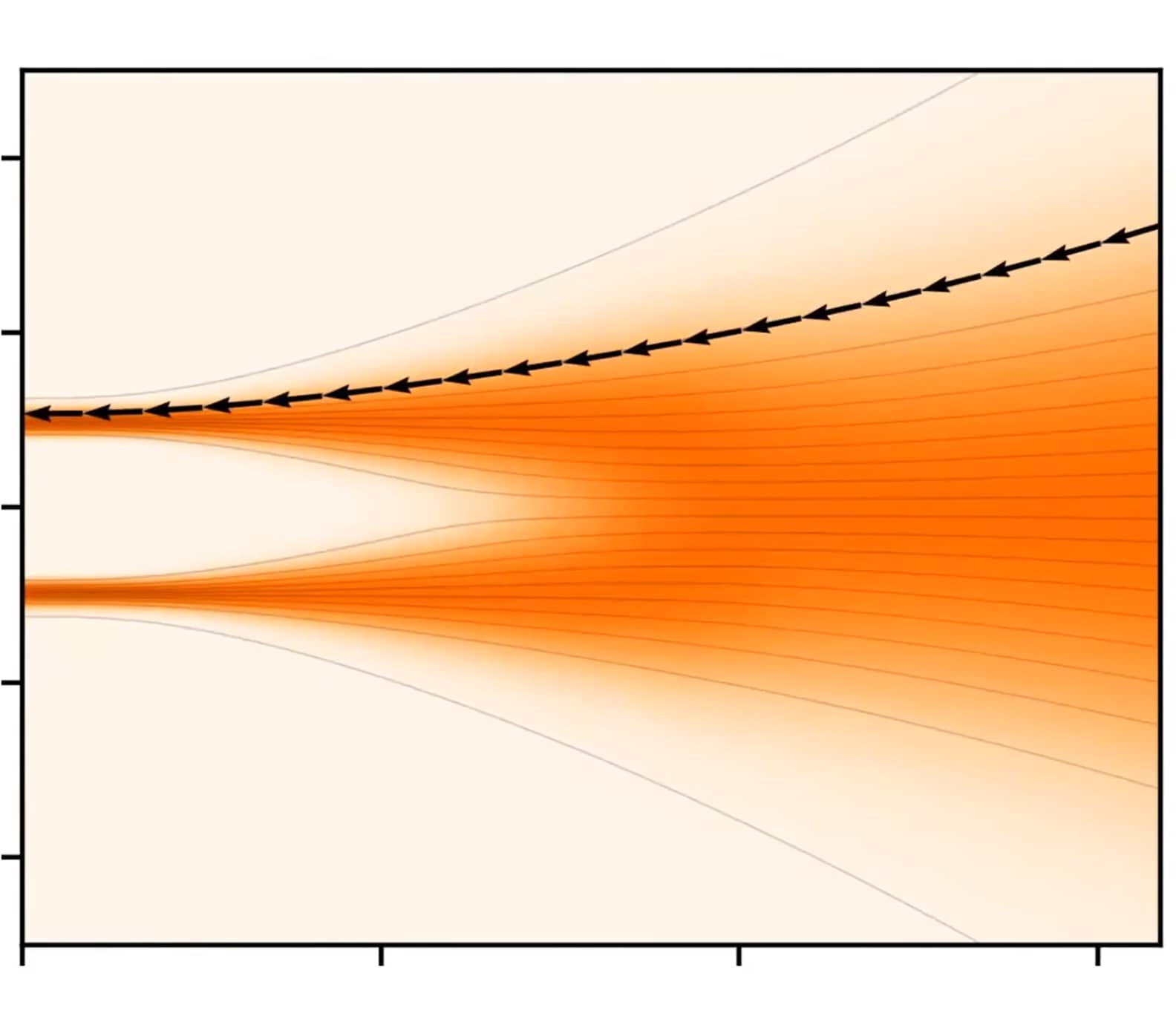轨迹

两种选择：

1. 在目标附近采用更短的步长；
2. 扭曲噪声调度，以在目标附近花费更多时间。

信号尺度问题

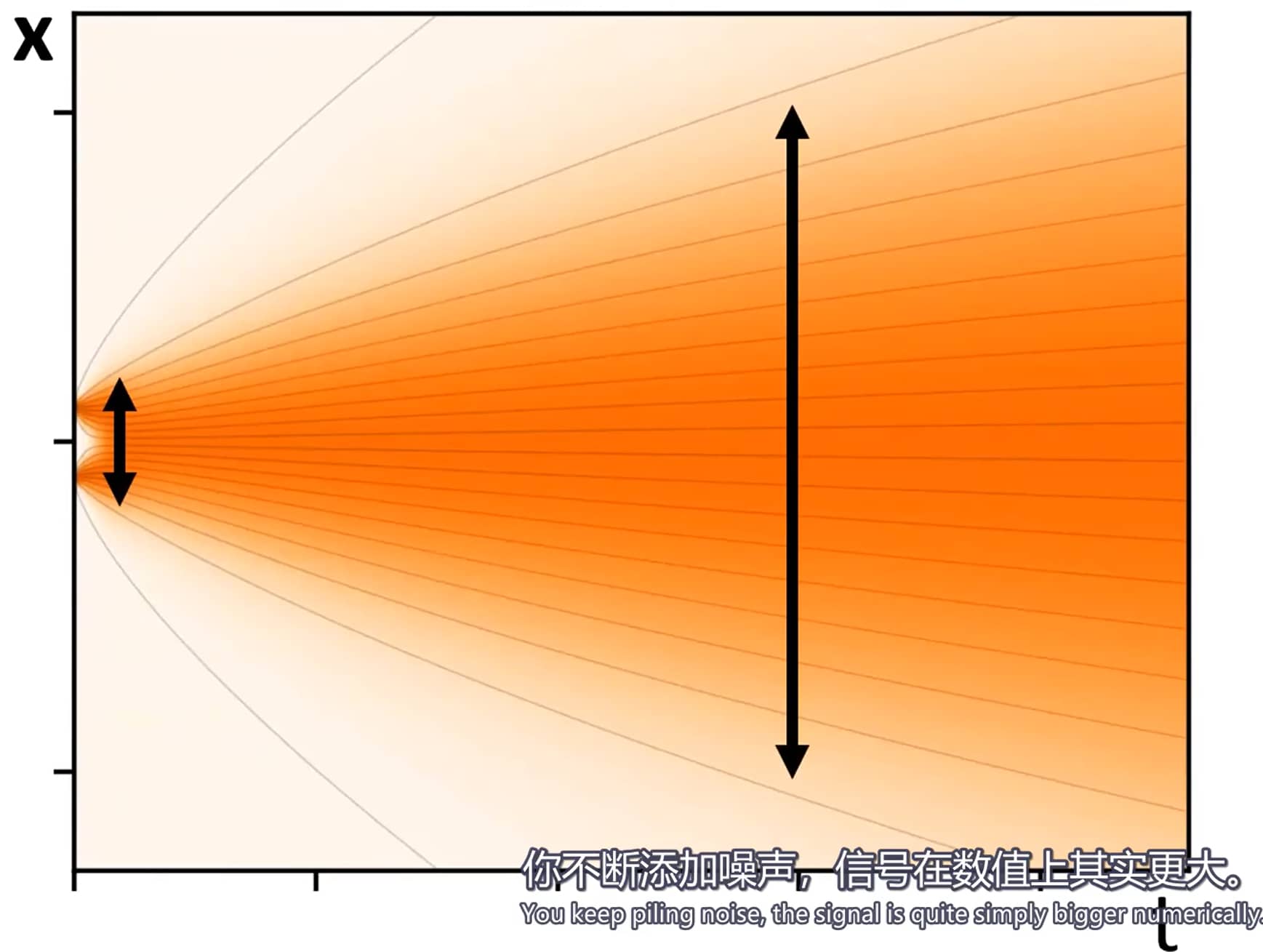
信号尺度差异过大会导致神经网络难以训练

确定性采样

不改变训练过程，只关注于采样过程。

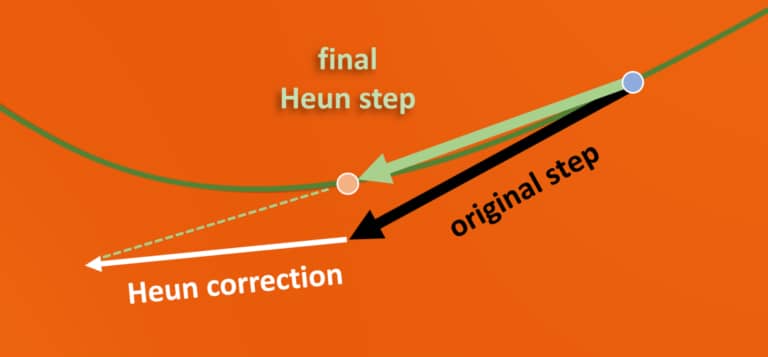改进Heun步

$$\mathrm{d}\boldsymbol{x}_\pm = \underbrace{ \textcolor{lime}{-\dot{\sigma}(t)\sigma(t)\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x}; \sigma(t)) \,\mathrm{d}t} }_{\text{probability flow ODE}} \pm \underbrace{ \textcolor{orange}{\beta(t)\sigma(t)^2\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x}; \sigma(t)) \,\mathrm{d}t} + \textcolor{cyan}{\sqrt{2\beta(t)}\sigma(t) \,\mathrm{d}\omega_t} }_{\substack{\text{Langevin diffusion SDE} \\ \text{(deterministic noise decay + noise injection)}}}$$

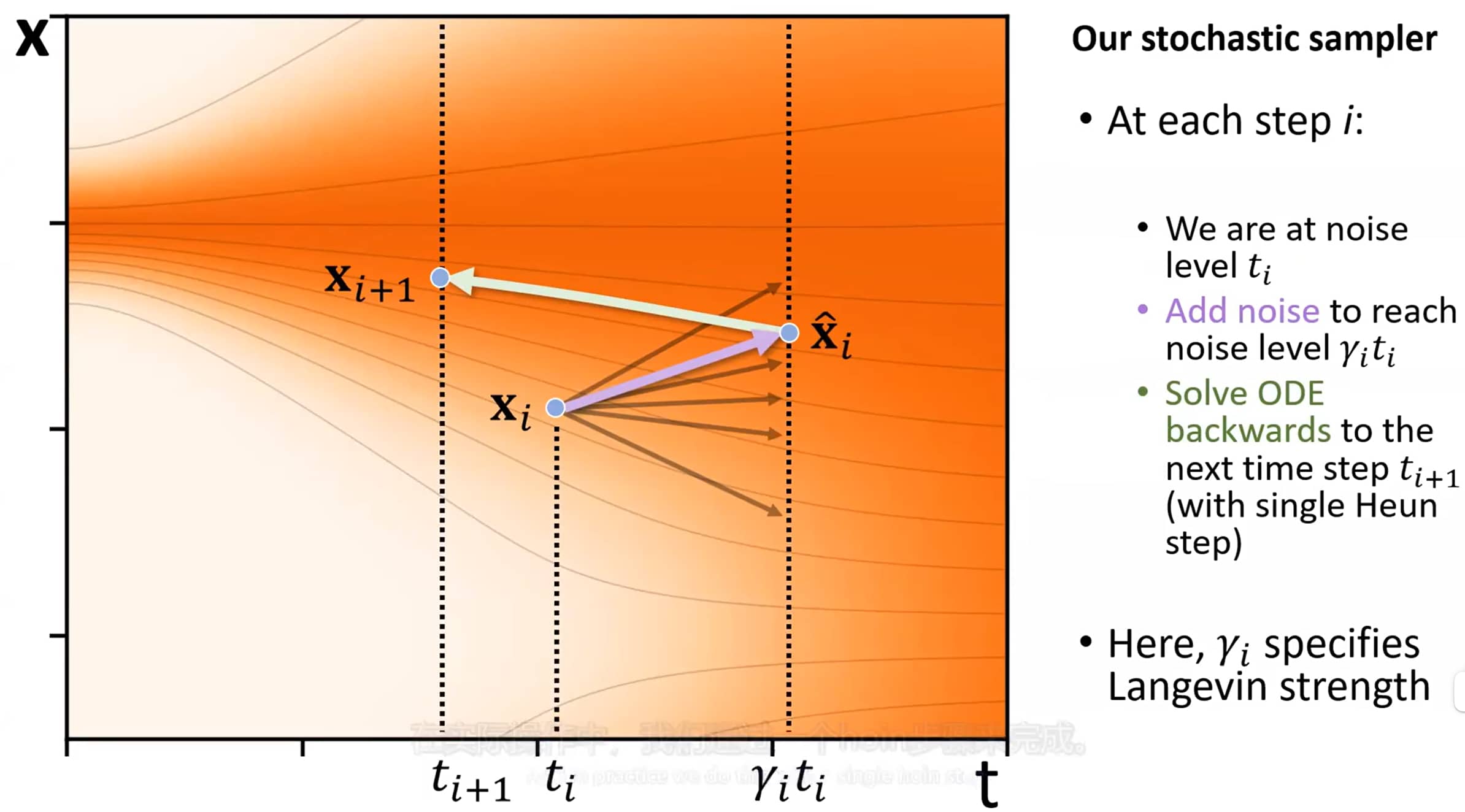
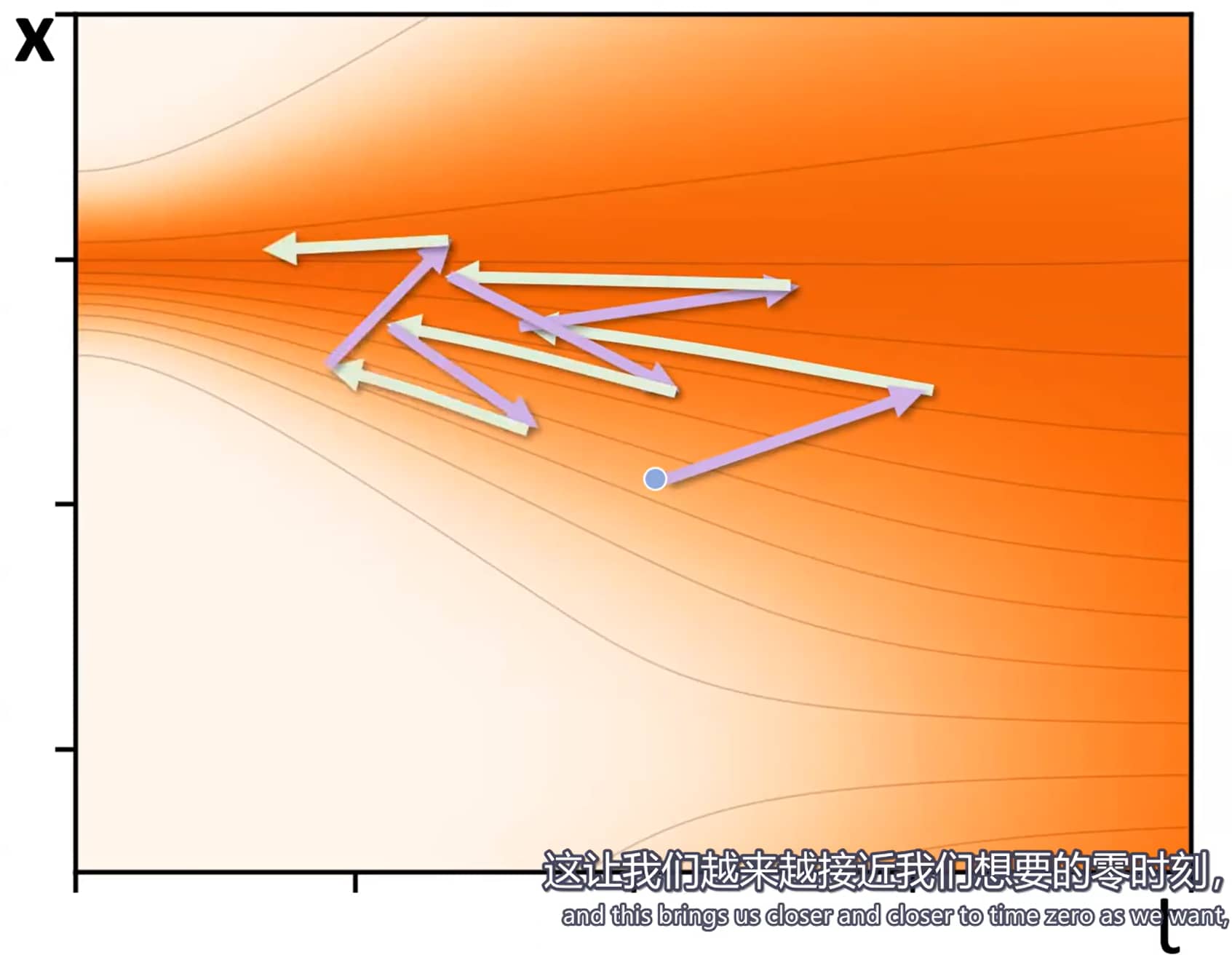纠偏过程

随机采样

预处理与训练

回顾两个误差来源：

• 采样中的离散化步骤

  • 我们已通过预训练网络研究了这一点

• 不准确的神经去噪器（又名得分函数）
  接下来的工作：

  • 改进网络预处理（例如，输入和输出缩放）
  • 改进训练（损失缩放，以及在哪些噪声水平上训练？）

• 我们不会（大幅）改变层架构等。

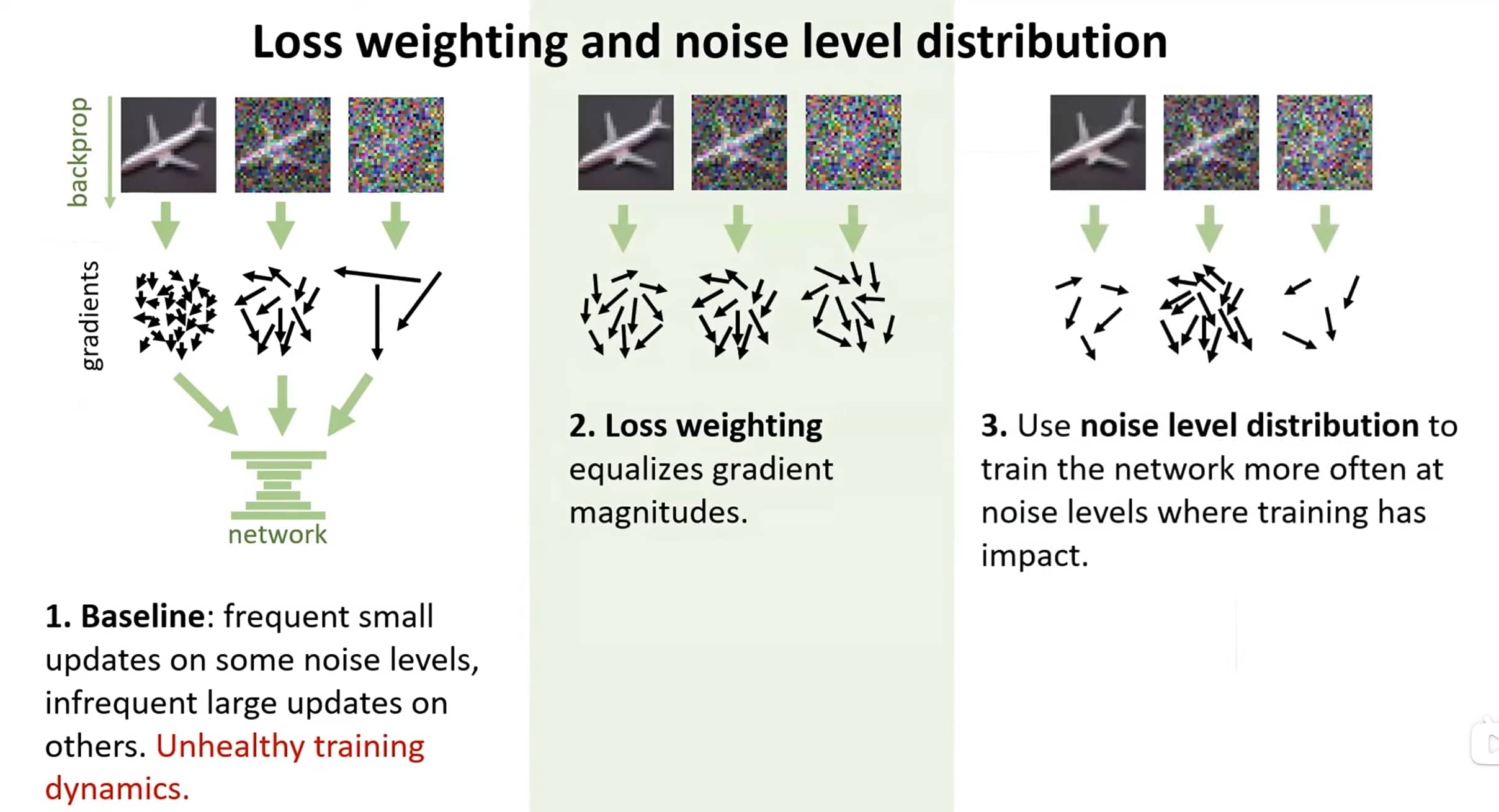
Preconditioning

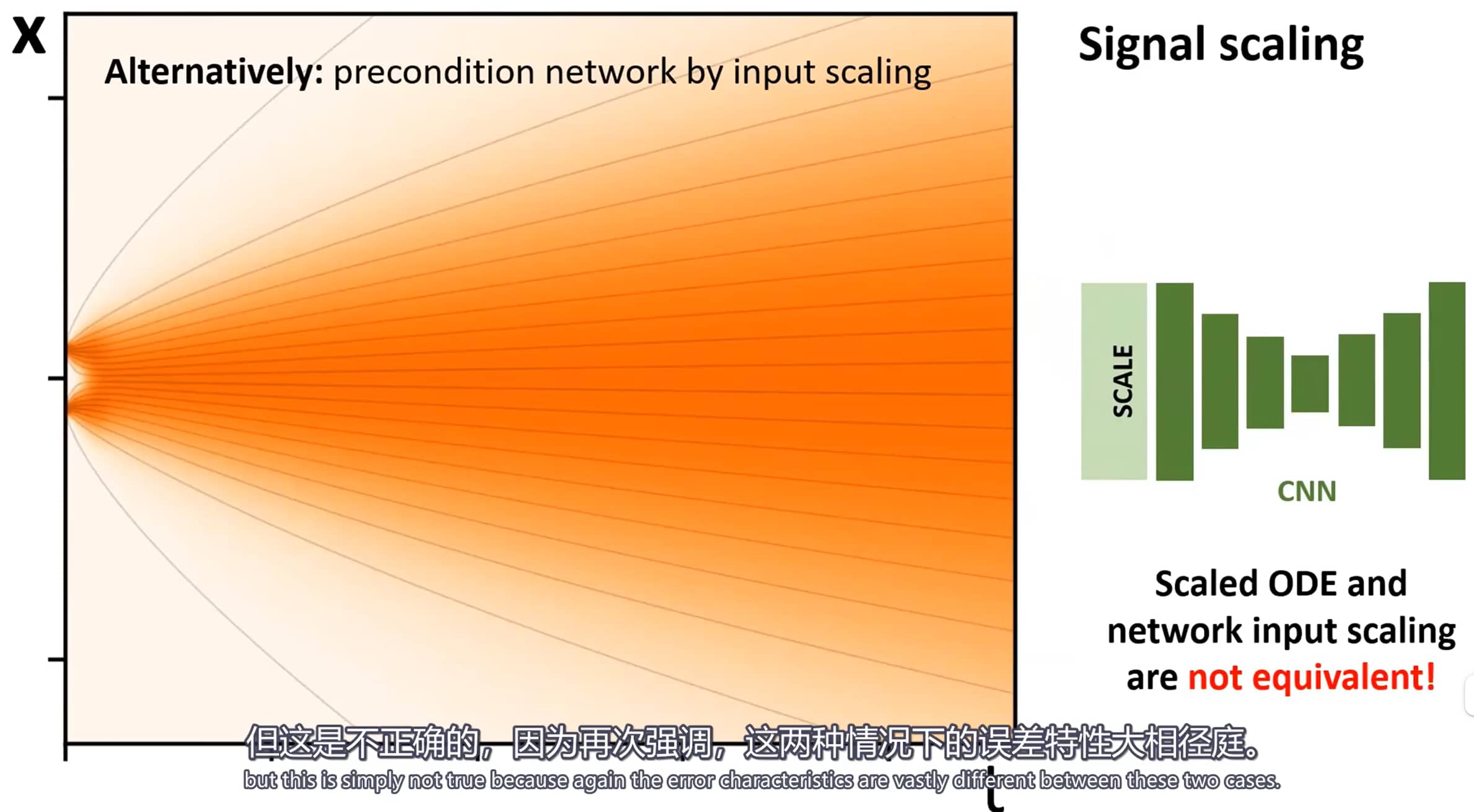
• 为了让CNN更易处理：

  • (A) 始终向网络输入 单位标准差的输入（unit stdev inputs）
  • (B) ……并使用 单位标准差的目标（unit stdev targets）进行训练

• 网络会产生误差。我们应当：

  • © 最小化网络对去噪器输出的贡献

• 我们的噪声水平变化极大，因此这一点至关重要！

改进Heun步

• 扩散模型的模块化设计

  • 训练、采样与网络架构并非紧密耦合

• 精心设计每个“模块”可带来显著改进

• 随机性是把双刃剑

• 更高分辨率、网络架构、条件设定/引导、大规模数据集……？

  • 已成熟到可对基础理论开展系统性分析

数学推导

Song等人将其前向SDE定义为：

$$\mathrm{d}\boldsymbol{x} = \boldsymbol{f}(\boldsymbol{x}, t)\mathrm{d}t + g(t)\mathrm{d}\omega_t$$

其中

• $\omega_t$ 是标准维纳过程（Wiener process）；
• $\boldsymbol{f}(\cdot, t): \mathbb{R}^d \to \mathbb{R}^d$ 为漂移系数；
• $g(\cdot): \mathbb{R} \to \mathbb{R}$ 为扩散系数
• $d$ 为数据集维度。

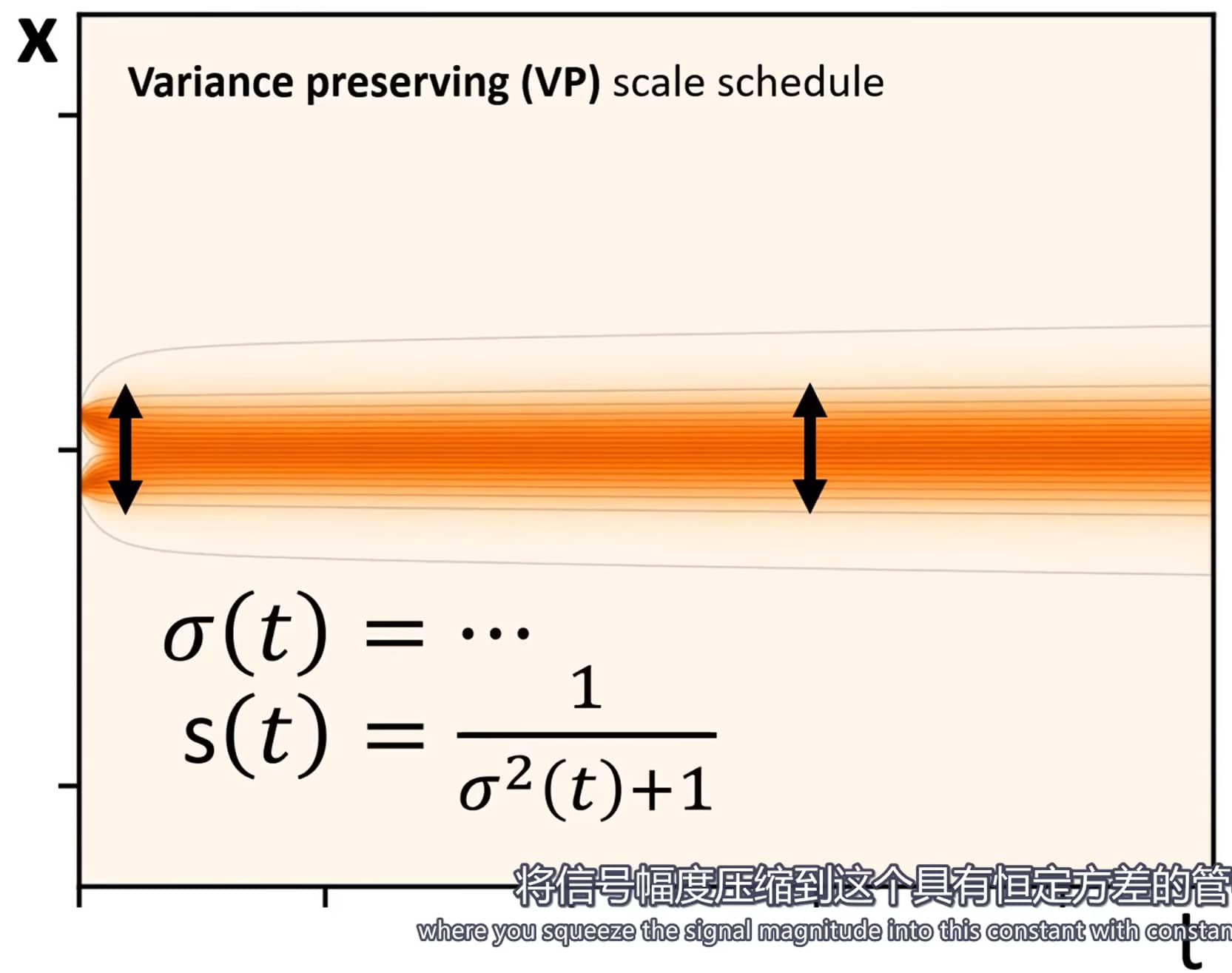
在 方差保持（VP） 和 方差爆炸（VE） 公式中，这两个系数的选择不同；且 $\boldsymbol{f}(\cdot, t)$ 始终具有 $\boldsymbol{f}(\boldsymbol{x}, t) = f(t)\boldsymbol{x}$ 的形式（其中 $f(\cdot): \mathbb{R} \to \mathbb{R}$）。因此，该SDE可等价改写为：

$$\mathrm{d}\boldsymbol{x} = f(t)\boldsymbol{x}\mathrm{d}t + g(t)\mathrm{d}\omega_t$$

该SDE的扰动核具有如下一般形式：

$$p_{0t}(\boldsymbol{x}(t) \mid \boldsymbol{x}(0)) = \mathcal{N}\big(\boldsymbol{x}(t);\ s(t)\boldsymbol{x}(0),\ s^2(t)\sigma^2(t)\boldsymbol{I}\big)$$

其中 $\mathcal{N}(\boldsymbol{x};\ \boldsymbol{\mu},\ \boldsymbol{\Sigma})$ 表示均值为 $\boldsymbol{\mu}$、协方差为 $\boldsymbol{\Sigma}$ 的高斯分布在 $\boldsymbol{x}$ 处的概率密度函数，且：

$$s(t) = \exp\left( \int_0^t f(\xi)\mathrm{d}\xi \right), \quad \sigma(t) = \sqrt{ \int_0^t \frac{g^2(\xi)}{s^2(\xi)} \mathrm{d}\xi }$$

边缘分布 $p_t(\boldsymbol{x})$ 可通过对初始状态 $\boldsymbol{x}(0)$ 积分扰动核得到：

$$p_t(\boldsymbol{x}) = \int_{\mathbb{R}^d} p_{0t}(\boldsymbol{x} \mid \boldsymbol{x}_0)\, p_{\text{data}}(\boldsymbol{x}_0)\,\mathrm{d}\boldsymbol{x}_0$$

Song等人[[49]]定义了 概率流ODE，使其服从上述相同的边缘分布 $p_t(\boldsymbol{x})$：

$$\mathrm{d}\boldsymbol{x} = \left[ f(t)\boldsymbol{x} - \frac{1}{2}g(t)^2 \nabla_{\boldsymbol{x}} \log p_t(\boldsymbol{x}) \right] \mathrm{d}t$$

原始ODE公式（式14）围绕函数 $f$ 和 $g$ 构建，这两个函数直接对应公式中的特定项；而边缘分布的性质（式12）只能通过这些函数间接推导。然而，$f$ 和 $g$ 本身的实际意义有限，相比之下，边缘分布在 模型训练、采样过程初始化，以及理解ODE实际行为等方面都至关重要。

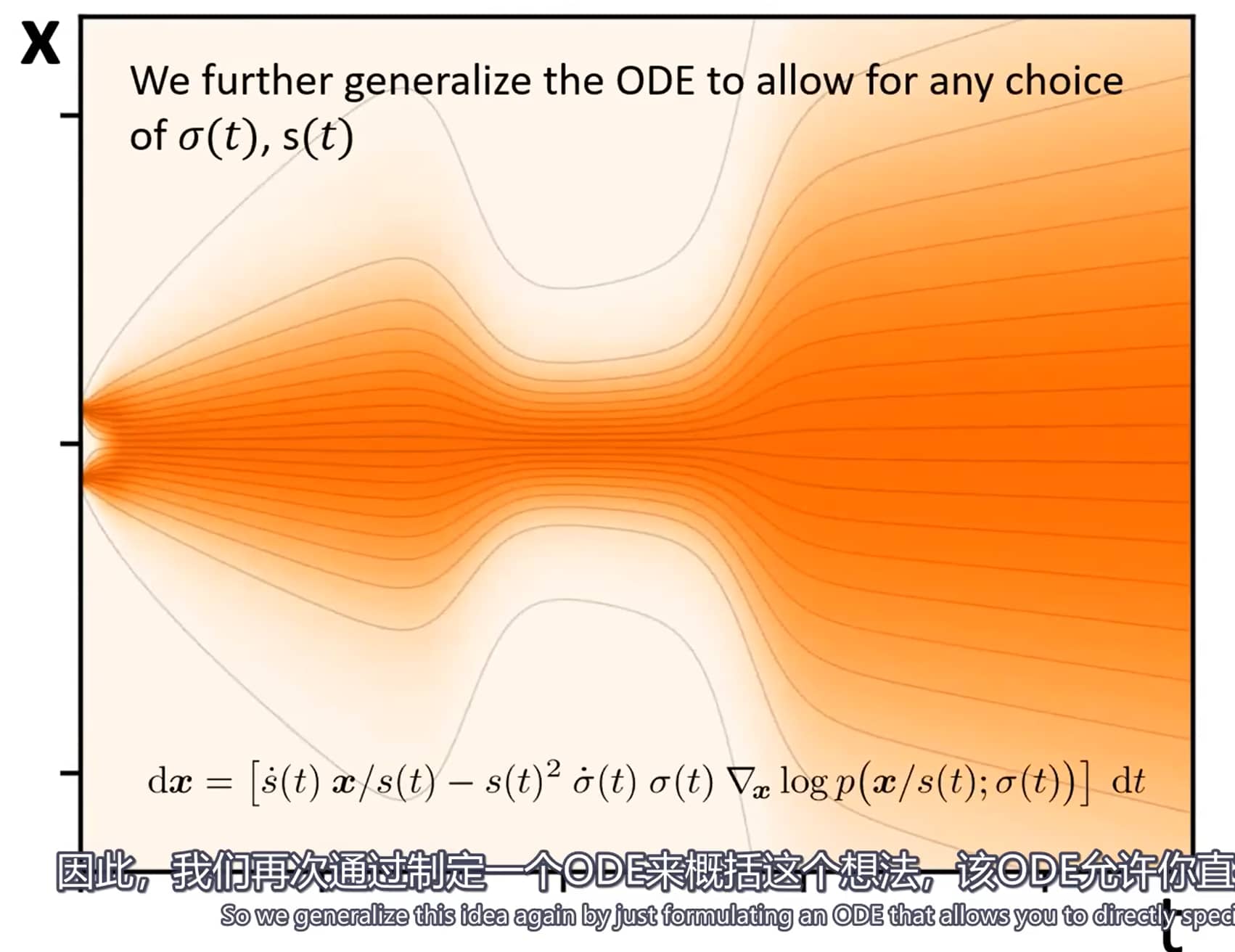
由于概率流ODE的核心思想是匹配一组特定的边缘分布，将边缘分布视为“一等公民”，并直接基于 $\sigma(t)$ 和 $s(t)$ 定义ODE（无需依赖 $f(t)$ 和 $g(t)$），是更合理的做法。

我们从式13的边缘分布闭式表达入手推导：

$$\begin{align*} p_t(\boldsymbol{x}) &= \int_{\mathbb{R}^d} p_{0t}(\boldsymbol{x} \mid \boldsymbol{x}_0)\, p_{\text{data}}(\boldsymbol{x}_0)\,\mathrm{d}\boldsymbol{x}_0 \\ &= \int_{\mathbb{R}^d} p_{\text{data}}(\boldsymbol{x}_0) \, \mathcal{N}\big(\boldsymbol{x};\ s(t)\boldsymbol{x}_0,\ s(t)^2\sigma(t)^2\boldsymbol{I}\big) \,\mathrm{d}\boldsymbol{x}_0 \\ &= \int_{\mathbb{R}^d} p_{\text{data}}(\boldsymbol{x}_0) \, \left[ s(t)^{-d} \mathcal{N}\big(\boldsymbol{x}/s(t);\ \boldsymbol{x}_0,\ \sigma(t)^2\boldsymbol{I}\big) \right] \,\mathrm{d}\boldsymbol{x}_0 \\ &= s(t)^{-d} \int_{\mathbb{R}^d} p_{\text{data}}(\boldsymbol{x}_0) \, \mathcal{N}\big(\boldsymbol{x}/s(t);\ \boldsymbol{x}_0,\ \sigma(t)^2\boldsymbol{I}\big) \,\mathrm{d}\boldsymbol{x}_0 \\ &= s(t)^{-d} \left[ p_{\text{data}} * \mathcal{N}\big(\boldsymbol{0},\ \sigma(t)^2\boldsymbol{I}\big) \right] \big(\boldsymbol{x}/s(t)\big) \end{align*}$$

其中 $p_a * p_b$ 表示概率密度函数 $p_a$ 和 $p_b$ 的卷积。方括号内的表达式对应对 $p_{\text{data}}$ 进行“平滑化”的结果（通过向样本添加独立同分布的高斯噪声实现）。我们将该分布记为 $p(\boldsymbol{x};\sigma)$：

$$p(\boldsymbol{x};\sigma) = p_{\text{data}} * \mathcal{N}\big(\boldsymbol{0},\ \sigma^2\boldsymbol{I}\big), \quad p_t(\boldsymbol{x}) = s(t)^{-d}\, p\big(\boldsymbol{x}/s(t);\ \sigma(t)\big)$$

现在，我们可以用 $p(\boldsymbol{x};\sigma)$ 代替 $p_t(\boldsymbol{x})$，重新表达概率流ODE（式14）：

$$\begin{align*} \mathrm{d}\boldsymbol{x} &= \left[ f(t)\boldsymbol{x} - \frac{1}{2}g(t)^2 \nabla_{\boldsymbol{x}} \log \big[ p_t(\boldsymbol{x}) \big] \right] \mathrm{d}t \\ &= \left[ f(t)\boldsymbol{x} - \frac{1}{2}g(t)^2 \nabla_{\boldsymbol{x}} \log \big[ s(t)^{-d}\, p\big(\boldsymbol{x}/s(t);\ \sigma(t)\big) \big] \right] \mathrm{d}t \\ &= \left[ f(t)\boldsymbol{x} - \frac{1}{2}g(t)^2 \left( \nabla_{\boldsymbol{x}} \log s(t)^{-d} + \nabla_{\boldsymbol{x}} \log p\big(\boldsymbol{x}/s(t);\ \sigma(t)\big) \right) \right] \mathrm{d}t \\ &= \left[ f(t)\boldsymbol{x} - \frac{1}{2}g(t)^2 \nabla_{\boldsymbol{x}} \log p\big(\boldsymbol{x}/s(t);\ \sigma(t)\big) \right] \mathrm{d}t \end{align*}$$