SDE视角下的生成模型（上）

2025/07/30 - 至今
待完善

主要参考资料

本篇文章主要基于《Score-board Generative Modeling Through Stochastic Differential Equations》Yang Song以及以下几个视频、博文。

相关数学推导主要来自：B站讲解 Nik_Li - 一个视频看懂如何从SDE视角看生成模型、苏剑林-科学空间-一般框架之SDE篇

PPT截图、整体脉络主要来自：Yang Song的讲座 B站 -【斯坦福大学Yang Song-当随机微分方程SDE遇上生成扩散模型】 和 blog

概述

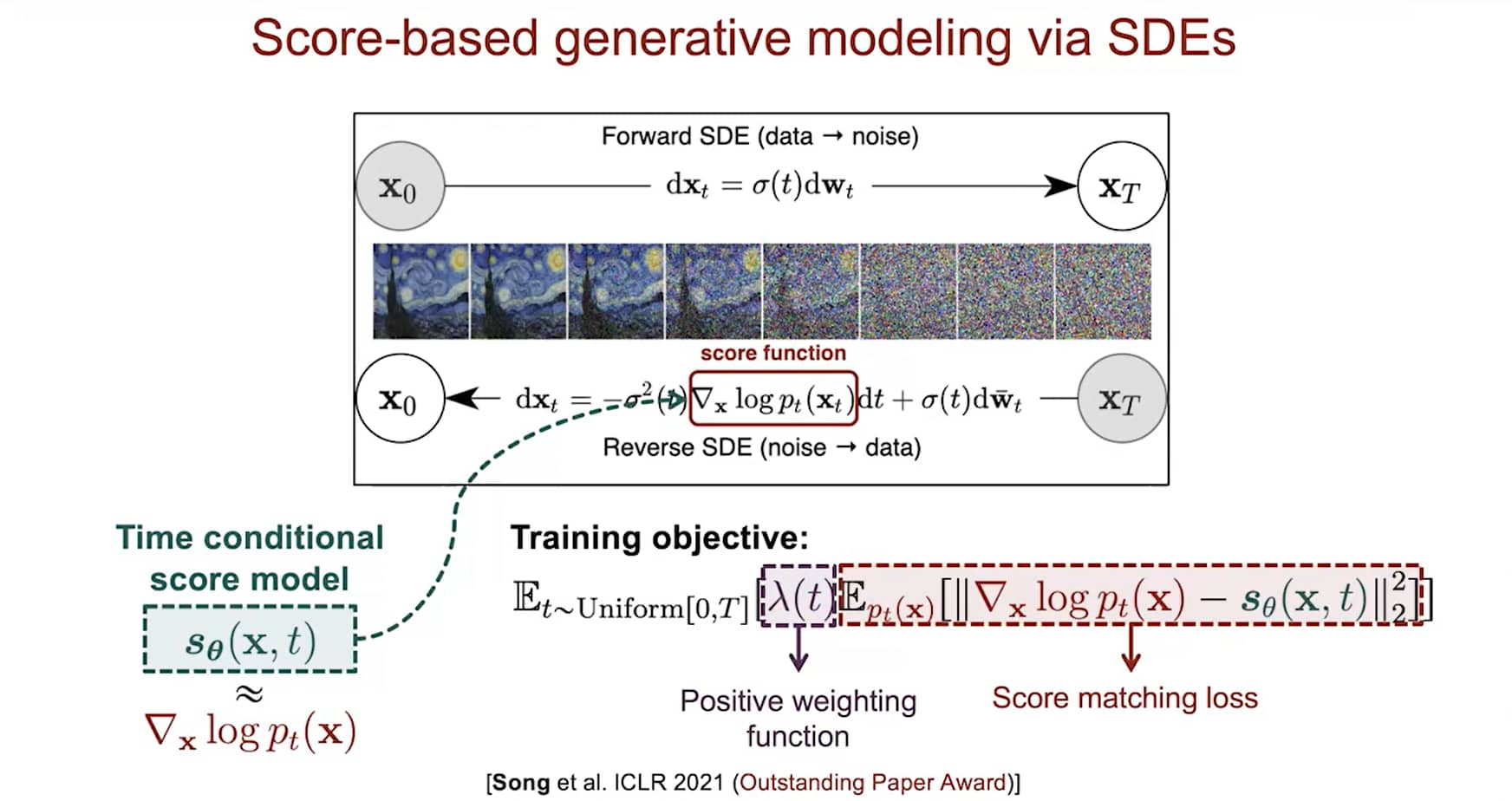用SDEs架构对score-based model建模

• Time-dependent score-based model

  $$s_\theta(\mathbf{x}, t) \approx \nabla_\mathbf{x} \log p_t(\mathbf{x})$$

• Training

  $$\mathbb{E}_{t \in \mathcal{U}(0,T)} \left[ \lambda(t) \mathbb{E}_{p_t(\mathbf{x})} \left[ \left\| \nabla_\mathbf{x} \log p_t(\mathbf{x}) - s_\theta(\mathbf{x}, t) \right\|_2^2 \right] \right]$$

• Reverse-time SDE

  $$d\mathbf{x} = -\sigma^2(t) s_\theta(\mathbf{x}, t) dt + \sigma(t) d\bar{\mathbf{w}}$$

• Euler-Maruyama (analogous to Euler for ODEs)

  $$\begin{align*} \mathbf{x} &\leftarrow \mathbf{x} - \sigma(t)^2 s_\theta(\mathbf{x}, t) \Delta t + \sigma(t) \, \mathbf{z} \quad (\mathbf{z} \sim \mathcal{N}(\mathbf{0}, |\Delta t| \, \mathbf{I})) \\ t &\leftarrow t + \Delta t \end{align*}$$

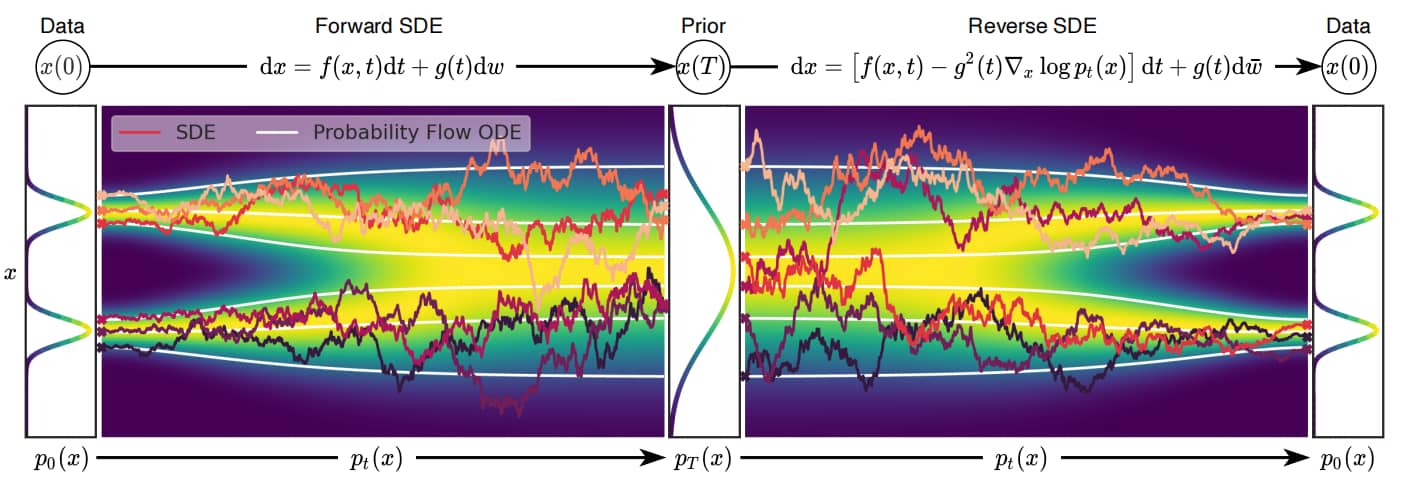基于分数的SDE生成建模示意图。我们可以通过 SDE 将 data 映射到noise distribution（prior distribution），并通过逆向 SDE 实现生成建模。同时也可以逆向求解关联概率流ODE，这将产生一个确定性过程，其采样结果与SDE具有相同分布。无论是逆向时间随机微分方程还是概率流ODE，都可以通过估计score function 来获得

知识准备

Wiener过程（布朗运动）：

$$W(t) \sim N(0,t)$$

Wiener过程的增量具有正态性，因此有差分方程：

$$W(t+\Delta t) - W(t) \sim N(0, \Delta t), \quad \Delta t \to 0$$

取极限，得到微分方程：

$$d W = \sqrt{d t} Z, \quad Z \sim N(0,1)$$

假设经扩散过程，data distribution $\to$ prior distribution（$p$）。有伊藤过程（扩散过程）前向过程的SDE：

$$d\mathbf{x} = \mathbf{f}(\mathbf{x},t)dt + g(t)d W$$

其中

• $\mathbf{x}$：状态变量
• $\mathbf{f}$：漂移系数，用于控制随机过程的确定性质。
• $g(t)$：扩散系数
• $W(t)$：Wiener过程

已知 $\mathbf{f},g,p$，有逆向过程的SDE：

$$d\mathbf{x} = \left[\mathbf{f}(\mathbf{x}_t, t) - g^2(t) \nabla_{\mathbf{x}} \log p(\mathbf{x})\right]dt + g(t)d w$$

• $\nabla_{\mathbf{x}} \log p(\mathbf{x})$ 即为 score function，用神经网络逼近之。

主干部分

Yang Song 本篇论文的主要贡献在于，其提出了一种SDE框架，并在此框架下统一了 DDPM（Denoising Diffusion Probabilistic Models）与 SMLD（Score Matching with Langevin Dynamics）这两种生成模型。

动机

<span style="color:red;">问题：NCSN使用的是有限噪声，在NCSN的框架上，如何引入无限噪声水平？如何将之前的离散过程连续化？

想法的可视化表达

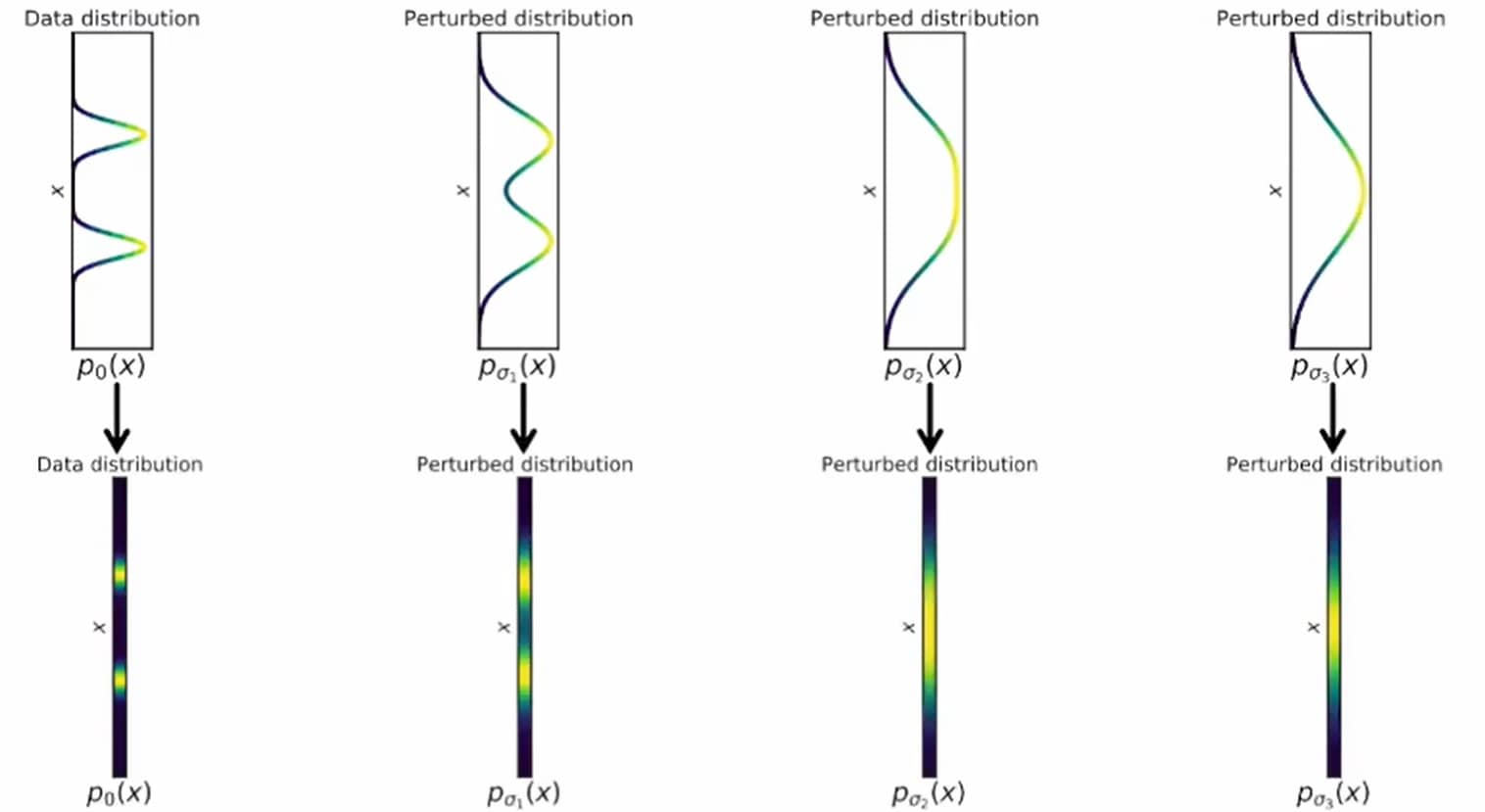
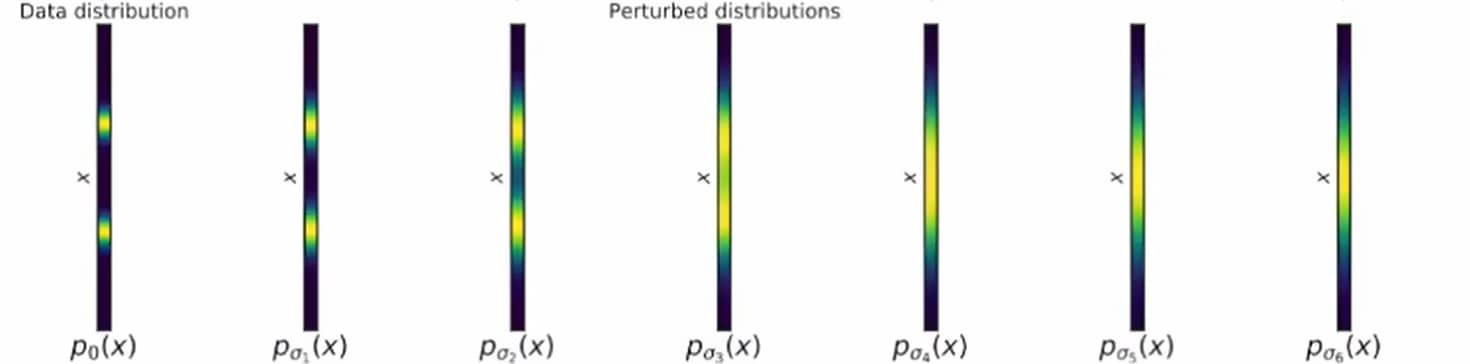
在此情况下，噪声扰动过程是一个连续时间随机过程，如下图所示。

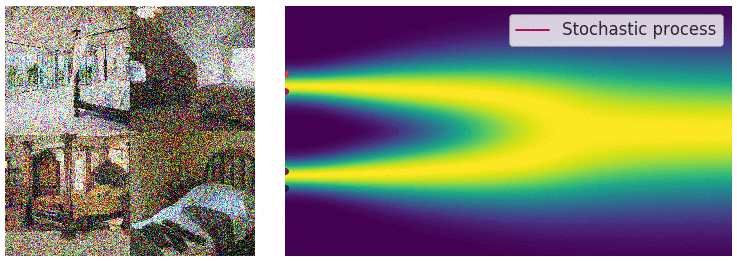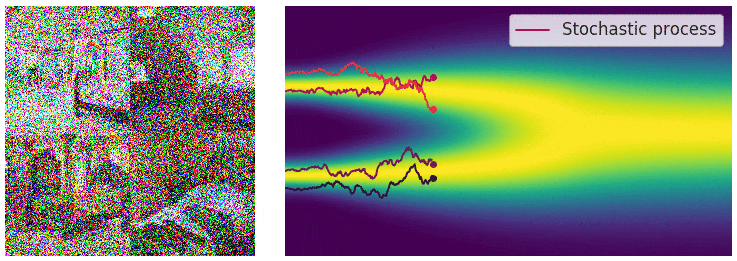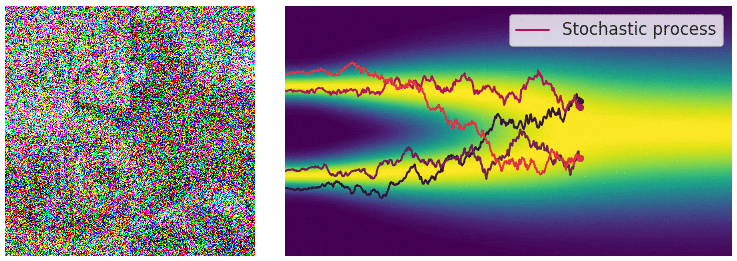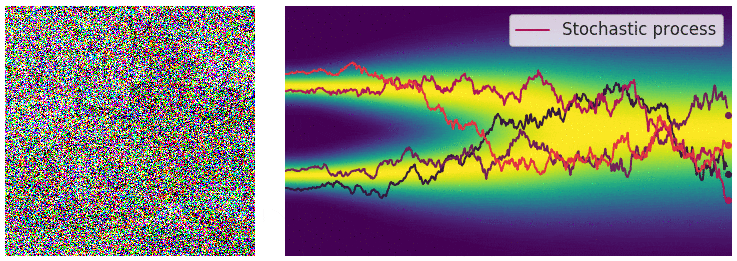通过连续时间随机过程将数据扰动至纯噪声

正向SDE的建立

<span style="color:red;">问题：如何简洁地表示一个随机过程？

许多随机过程（尤其是扩散过程）是随机微分方程（SDEs）的解。一般来说，SDE具有如下形式：

$$\mathrm{d}\mathbf{x} = \mathbf{f}(\mathbf{x}, t)\mathrm{d}t + g(t)\mathrm{d}\mathbf{w} \tag{1}$$

其中

• $\mathbf{f}(\cdot, t) : \mathbb{R}^d \to \mathbb{R}^d$ 是称为漂移系数 (drift coefficient) 的向量值函数，
• $g(t) \in \mathbb{R}$ 是称为扩散系数 (diffusion coefficient) 的实值函数，
• $\mathbf{w}$ 表示标准布朗运动，$\mathrm{d}\mathbf{w}$ 可视为无穷小的白噪声。

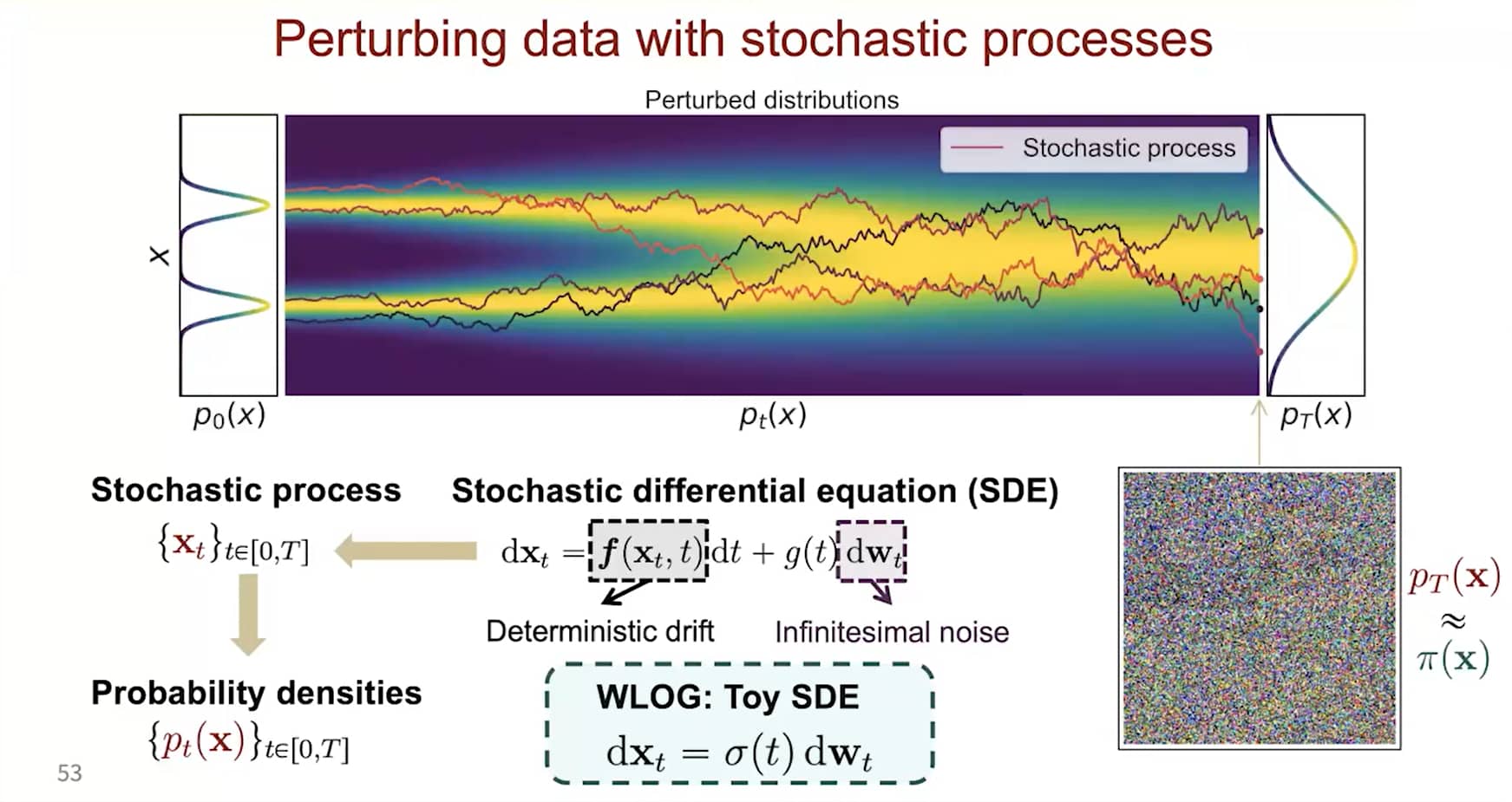用随机过程做扰动

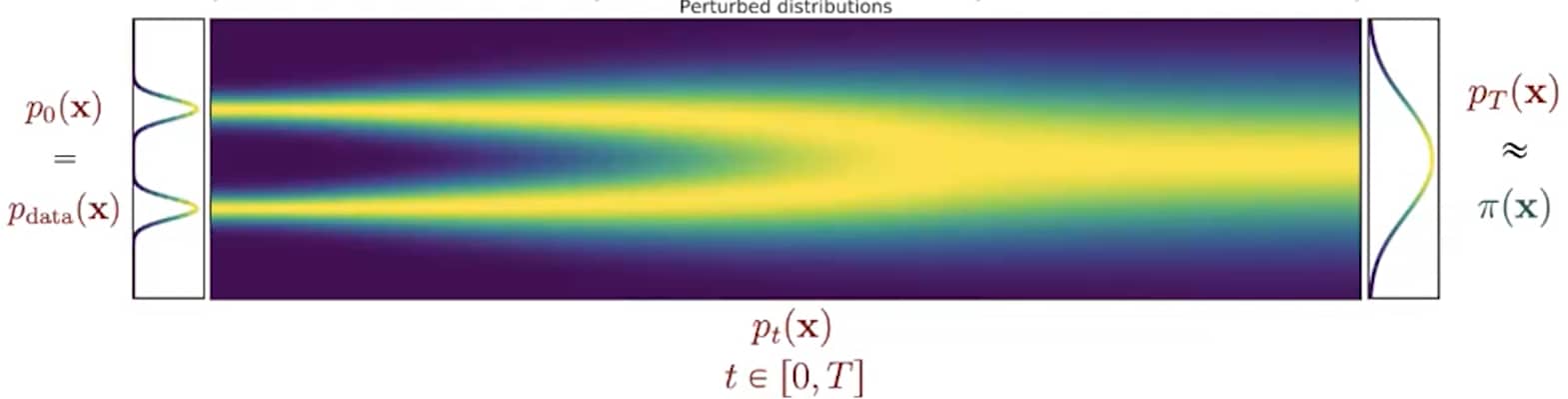
SDE 的解是随机变量的连续集合 $\{\mathbf{x}(t)\}_{t \in [0,T]}$。随着时间指标 $t$ 从起始时间 $0$ 增长到结束时间 $T$，这些随机变量会描绘出 随机轨迹。

令 $p_t(\mathbf{x})$ 表示 $\mathbf{x}(t)$ 的边缘概率密度函数。$p_0(\mathbf{x}) = p(\mathbf{x})$ 是数据分布，$p_T(\mathbf{x})$ 会趋近于一个易处理的噪声分布 $\pi(\mathbf{x})$，称为先验分布。

式 <a href="#eq:1" class="equation-ref">(1)</a> 中的 SDE 是人工设计的，类似于在有限噪声尺度时人工设计 $\sigma_1 < \sigma_2 < \cdots < \sigma_L$ 这样。添加噪声扰动的方法众多，SDE 的选择也不唯一。例如，以下 SDE：

$$\mathrm{d}\mathbf{x} = e^t \mathrm{d}\mathbf{w}$$

用 均值为零、方差指数增长 的高斯噪声扰动数据——这类似于当 $\sigma_1 < \sigma_2 < \cdots < \sigma_L$ 构成等比数列时，用 $\mathcal{N}(0, \sigma_1^2 I)$、$\mathcal{N}(0, \sigma_2^2 I)$、$\cdots$、$\mathcal{N}(0, \sigma_L^2 I)$ 扰动数据的过程。

因此，SDE 应被视为模型的一部分，就像 $\{\sigma_1, \sigma_2, \cdots, \sigma_L\}$ 一样。我们提供了三种对图像普遍有效的 SDE：方差爆炸 SDE（VE SDE）、方差保持 SDE（VP SDE） 和 sub-VP SDE。

反转SDE以采样

在有限噪声尺度下，我们可通过 退火朗之万动力学（annealed Langevin dynamics）反转扰动过程来生成样本——即利用朗之万动力学，依次从每个噪声扰动的分布中采样。对于无限噪声尺度，我们可类似地通过 反转SDE（reverse SDE）反转扰动过程，实现样本生成。

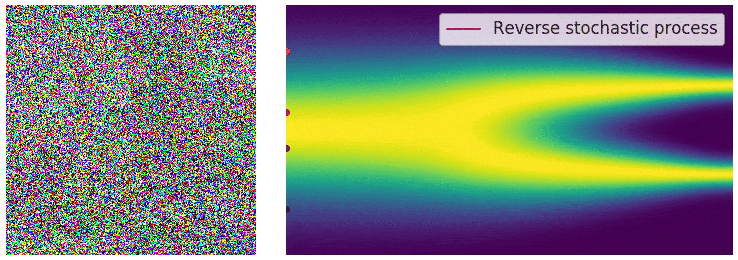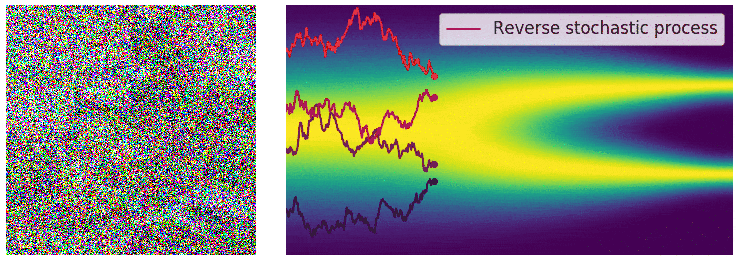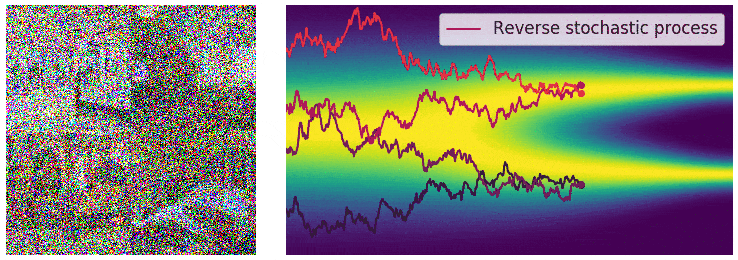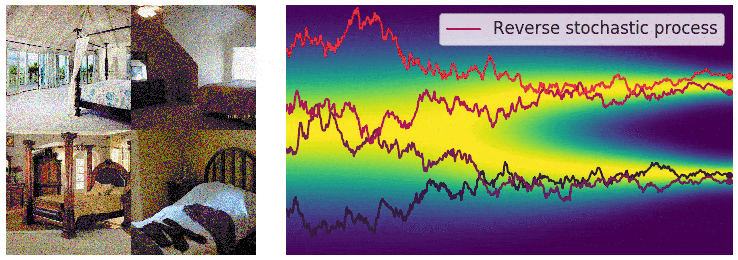通过反转扰动过程从噪声中生成样本

式 <a href="#eq:1" class="equation-ref">(1)</a> 中的 SDE 存在其对应的 反向SDE，其闭式解由文献 <sup><a href="#ref1">[1]</a></sup> 给出：

$$\mathrm{d}\mathbf{x} = \left[ \mathbf{f}(\mathbf{x}, t) - g^2(t) \nabla_{\mathbf{x}} \log p_t(\mathbf{x}) \right] \mathrm{d}t + g(t)\mathrm{d}\mathbf{w} \tag{2}$$

此处的 $\mathrm{d}t$ 表示 负无穷小时间步（因为逆SDE 需要 反向时间求解，即从 $t=T$ 到 $t=0$）。为计算上述反向SDE，需估计 $\nabla_{\mathbf{x}} \log p_t(\mathbf{x})$——这恰是 $p_t(\mathbf{x})$ 的 得分函数 (score function)。

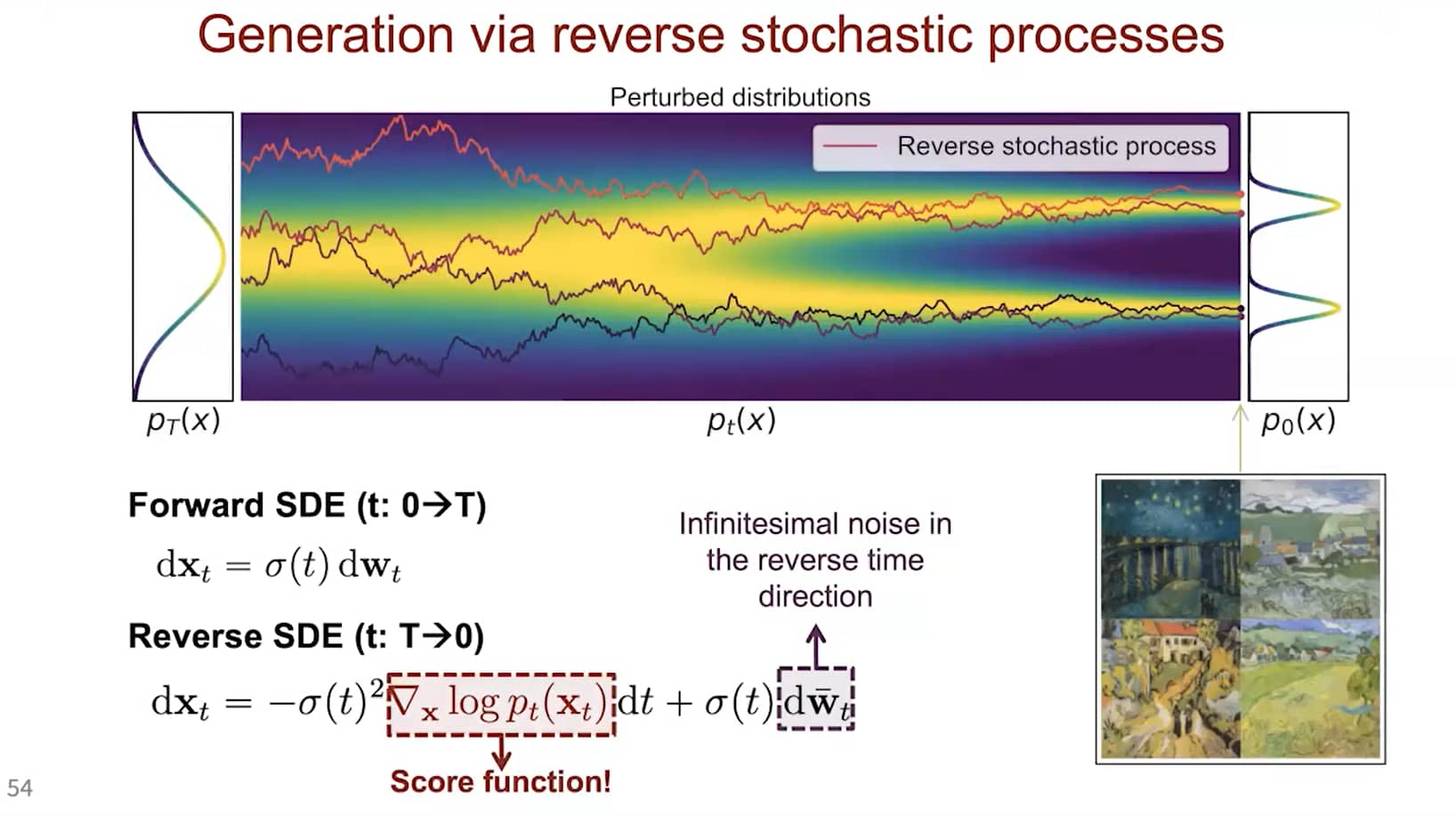用反向随机过程做生成

基于得分的模型与得分匹配估计逆SDE

求解逆SDE需要已知 (terminal distribution) 末端分布 $p_T(\mathbf{x})$ 和 得分函数 $\nabla_{\mathbf{x}} \log p_t(\mathbf{x})$。根据设计，前者接近完全可处理的 先验分布 $\pi(\mathbf{x})$，只需考虑后者。

为估计 $\nabla_{\mathbf{x}} \log p_t(\mathbf{x})$，我们训练 (Time-Dependent Score-Based Model) 时间依赖的得分模型 $s_\theta(\mathbf{x}, t)$，使得 $s_\theta(\mathbf{x}, t) \approx \nabla_{\mathbf{x}} \log p_t(\mathbf{x})$。这类似于有限噪声尺度下的 噪声条件得分模型 $s_\theta(\mathbf{x}, i)$（训练目标为 $s_\theta(\mathbf{x}, i) \approx \nabla_{\mathbf{x}} \log p_{\sigma_i}(\mathbf{x})$）。

$s_\theta(\mathbf{x}, t)$ 的训练目标是 Fisher散度的连续加权组合，形式为：

$$\mathbb{E}_{t \sim \mathcal{U}(0,T)} \bigl\{ \mathbb{E}_{p_t(\mathbf{x})} \left[ \lambda(t) \left\| \nabla_{\mathbf{x}} \log p_t(\mathbf{x}) - s_\theta(\mathbf{x}, t) \right\|_2^2 \right] \bigr\} \tag{3}$$

其中：

• $\mathcal{U}(0,T)$ 表示时间区间 $[0,T]$ 上的均匀分布；
• $\lambda: \mathbb{R} \to \mathbb{R}_{>0}$ 是正权重函数。

通常，我们选择 $\lambda(t) \propto 1/\mathbb{E}[\|\nabla_{\mathbf{x}(t)} \log p(\mathbf{x}(t) \mid \mathbf{x}(0))\|_2^2]$，以平衡不同时间步的得分匹配损失幅度。

与之前类似，Fisher散度的加权组合可通过 得分匹配方法（如去噪得分匹配、切片得分匹配）高效优化。当得分模型 $s_\theta(\mathbf{x}, t)$ 训练至最优后，将其代入 反向SDE 式 <a href="#eq:2" class="equation-ref">(2)</a> 中，即可得估计的反向SDE：

$$\mathrm{d}\mathbf{x} = \left[ \mathbf{f}(\mathbf{x}, t) - g^2(t) s_\theta(\mathbf{x}, t) \right] \mathrm{d}t + g(t)\mathrm{d}\mathbf{w}.$$

我们可从 $\mathbf{x}(T) \sim \pi$ 出发，求解上述 反向SDE 以得到样本 $\mathbf{x}(0)$。记通过该方式得到的 $\mathbf{x}(0)$ 的分布为 $p_\theta$。当得分模型 $s_\theta(\mathbf{x}, t)$ 训练良好时，$p_\theta \approx p_0$，此时 $\mathbf{x}(0)$ 是数据分布 $p_0$ 的近似样本。

如何求解反向SDE

通过数值SDE求解器求解估计的逆SDE，我们可以模拟逆向随机过程以生成样本。最简单的数值SDE求解器或许是 欧拉-丸山法（Euler-Maruyama method）。将其应用于我们的估计逆SDE时，它会通过有限时间步长和小高斯噪声对SDE进行离散化。具体来说，它会选择一个小的负时间步长 $\Delta t \approx 0$，初始化 $t \leftarrow T$，并迭代以下过程直至 $t \approx 0$：

$$\begin{align*} \Delta \mathbf{x} &\leftarrow \left[ \mathbf{f}(\mathbf{x}, t) - g^2(t) s_\theta(\mathbf{x}, t) \right] \Delta t + g(t) \sqrt{|\Delta t|} \mathbf{z}_t \\ \mathbf{x} &\leftarrow \mathbf{x} + \Delta \mathbf{x} \\ t &\leftarrow t + \Delta t, \end{align*}$$

其中 $\mathbf{z}_t \sim \mathcal{N}(0, \mathbf{I})$。欧拉-马尔雅那方法在定性上与朗之万动力学类似——两者都通过受高斯噪声扰动的得分函数更新 $\mathbf{x}$。

除欧拉-马尔雅那方法外，其他数值SDE求解器也可直接用于求解逆SDE以生成样本，例如 米尔斯坦方法（Milstein method）和 随机龙格-库塔方法（stochastic Runge-Kutta methods）。在文献中，我们提出了一种类似欧拉-马尔雅那的逆向扩散求解器，但更适配逆向时间SDE的求解。近年来，文献的作者引入了自适应步长SDE求解器，可更快生成更高质量的样本。

此外，我们的逆SDE具有两个特殊性质，支持更灵活的采样方法：

1. 我们通过时间依赖的得分模型 $s_\theta(\mathbf{x}, t)$，得到了 $\nabla_{\mathbf{x}} \log p_t(\mathbf{x})$ 的估计。
2. 我们仅关心从每个边缘分布 $p_t(\mathbf{x})$ 中采样。不同时间步的样本可具有任意相关性，无需形成逆SDE的特定轨迹。

基于这两个性质，我们可应用 MCMC方法 对数值SDE求解器得到的轨迹进行微调。具体来说，我们提出 预测-校正采样器（Predictor-Corrector samplers）：

• 预测器（Predictor）：可为任意数值SDE求解器，用于从现有样本 $\mathbf{x}(t) \sim p_t(\mathbf{x})$ 预测 $\mathbf{x}(t+\Delta t) \sim p_{t+\Delta t}(\mathbf{x})$。
• 校正器（Corrector）：可为任意仅依赖得分函数的MCMC过程，例如朗之万动力学（Langevin dynamics）或哈密顿蒙特卡洛（Hamiltonian Monte Carlo）。

在预测-校正采样器的每一步：

1. 首先用预测器选择合适的负步长 $\Delta t < 0$，并基于当前样本 $\mathbf{x}(t)$ 预测 $\mathbf{x}(t+\Delta t)$；
2. 然后运行若干校正步骤，根据得分模型 $s_\theta(\mathbf{x}, t+\Delta t)$ 改进 $\mathbf{x}(t+\Delta t)$，使其成为 $p_{t+\Delta t}(\mathbf{x})$ 的更高质量样本。

结合预测-校正方法与更优的得分模型架构，我们可在CIFAR-10数据集上实现当前最优的样本质量（通过FID和Inception分数衡量），超越了目前最先进的GAN模型（StyleGAN2 + ADA）。

概率流ODE（Probability Flow ODE）

尽管基于朗之万MCMC和SDE求解器的采样器能生成高质量样本，但它们无法为基于得分的生成模型计算 精确对数似然。接下来，我们介绍一种基于 常微分方程（ODE） 的采样器，它支持精确似然计算。

在文献中，我们证明：任意SDE都可转换为不改变其边缘分布 $\{p_t(\mathbf{x})\}_{t \in [0,T]}$ 的ODE。因此，通过求解该ODE，我们能从与逆SDE相同的分布中采样。SDE对应的ODE称为 概率流ODE，形式为[[21]]：

$$\mathrm{d}\mathbf{x} = \left[ \mathbf{f}(\mathbf{x}, t) - \frac{1}{2} g^2(t) \nabla_{\mathbf{x}} \log p_t(\mathbf{x}) \right] \mathrm{d}t. \tag{14}$$

下图展示了SDE和概率流ODE的轨迹。尽管ODE轨迹比SDE轨迹 明显更平滑，但它们会将相同的数据分布转换为相同的先验分布（反之亦然），共享同一组边缘分布 $\{p_t(\mathbf{x})\}_{t \in [0,T]}$。换言之，求解概率流ODE得到的轨迹，与SDE轨迹具有 相同的边缘分布。

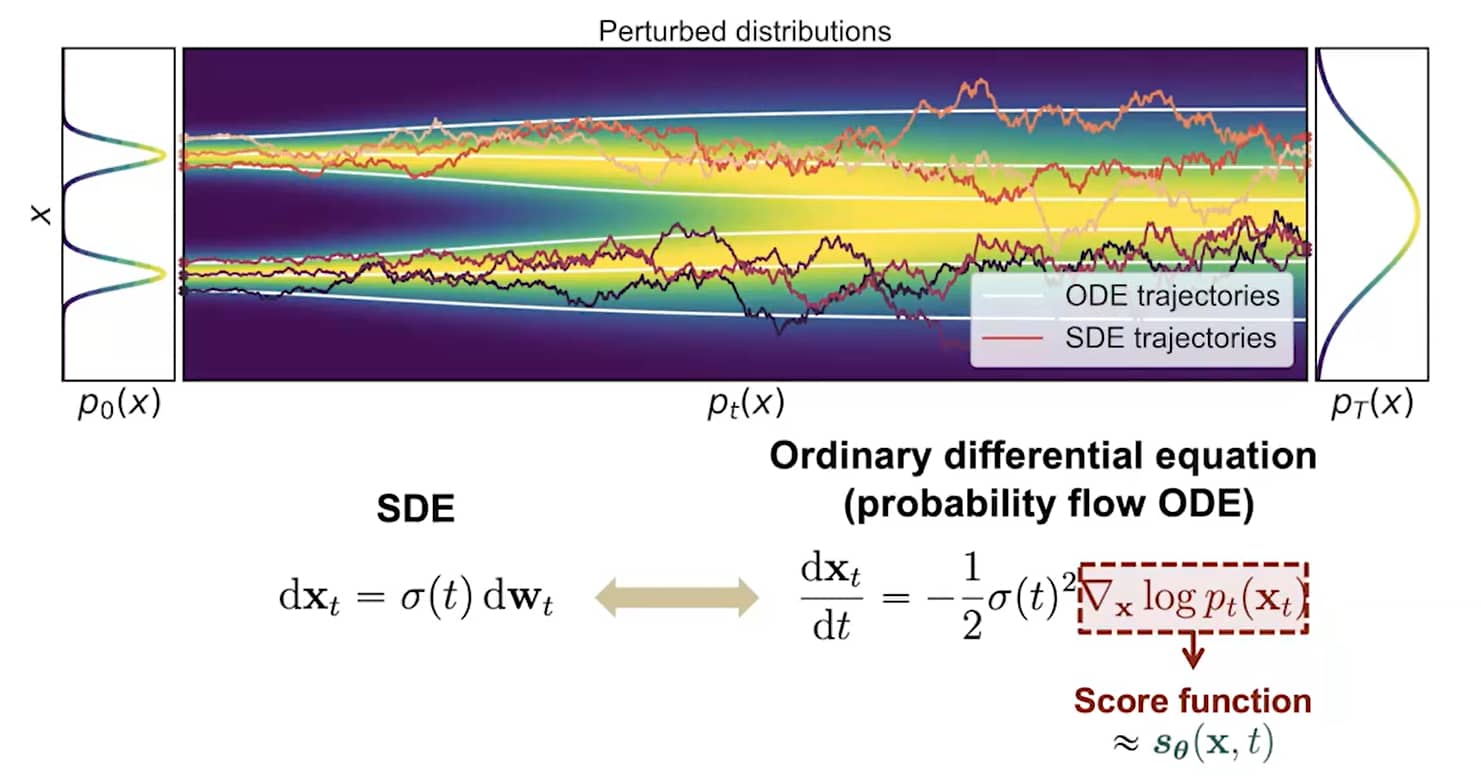SDE转化为ODE

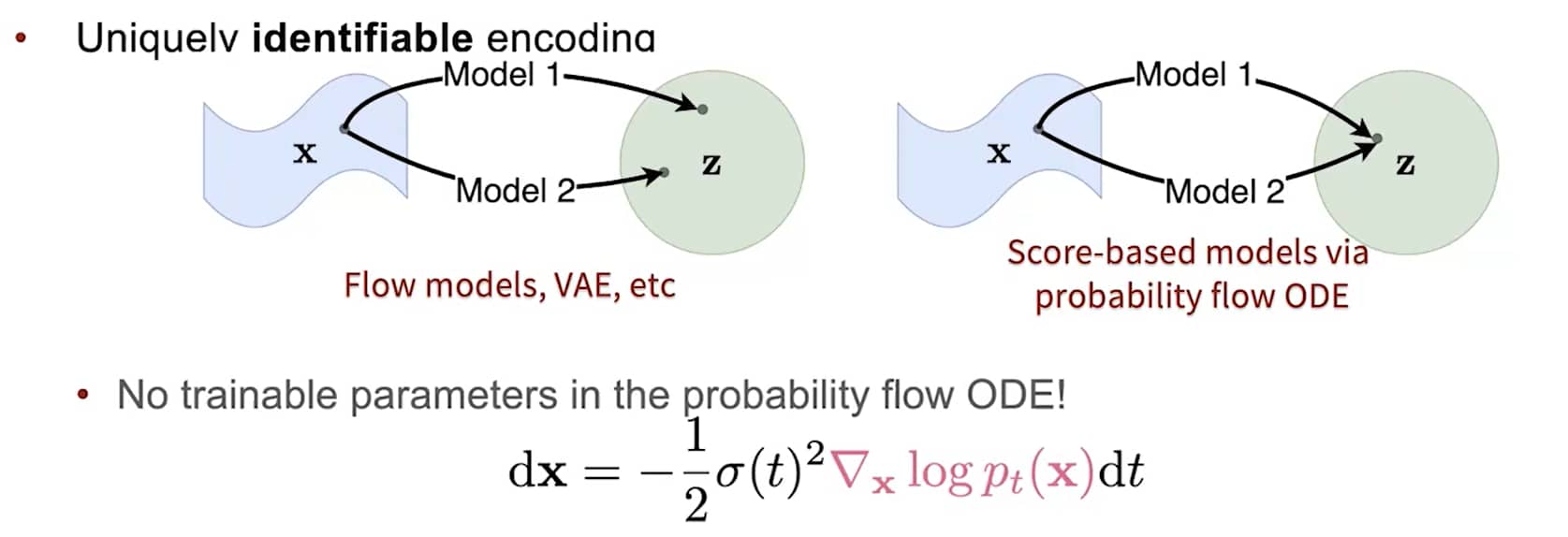概率流ODE具有唯一可识别编码的特性(uniquely identifible encoding)

使用ODE计算精确似然

概率流ODE的独特优势

概率流ODE的公式化表达具有若干独特优势：

当 $\mathbf{\nabla_{\mathbf{x}} \log p_t(\mathbf{x})}$ 被其近似 $s_\theta(\mathbf{x}, t)$ 替代时，概率流ODE成为 神经ODE（neural ODE） 的特例。具体而言，它是 连续归一化流（continuous normalizing flows） 的示例——因为概率流ODE会将数据分布 $p_0(\mathbf{x})$[[40]][[41]] 转换为先验噪声分布 $p_T(\mathbf{x})$（由于与SDE共享相同边缘分布），且 完全可逆。

因此，概率流ODE继承了神经ODE或连续归一化流的所有性质，包括 精确对数似然计算。具体来说，我们可利用 瞬时变量变换公式（文献 [[21]] 中的定理1、相关文献中的公式(4)），通过数值ODE求解器，从已知的先验密度 $p_T$ 计算未知的数据密度 $p_0$。

实际上，我们的模型在 均匀去量化的CIFAR-10图像 上实现了 当前最优的对数似然——甚至无需最大化似然训练。

当使用前文讨论的 似然加权（likelihood weighting） 训练基于得分的模型，并通过 变分去量化（variational dequantization） 计算离散图像的似然时，我们的模型可实现与“当前最优自回归模型” 相当甚至更优的似然（且无需任何数据增强）。

这是一段需要引用文献的内容 <sup><a href="#ref1">1</a></sup>，
另一段引用<sup><a href="#ref2">2</a></sup>。

参考文献

• [1] Reverse-time diffusion equation models
  B.D. Anderson. Stochastic Processes and their Applications, Vol 12(3), pp. 313--326. Elsevier. 1982.
• [2] 霍金 S. 时间简史[M]. bantam, 2005.

待修改。