PDE笔记-第二讲（上）

守恒律 = 动量守恒 + 能量守恒 + 质量守恒

动量守恒

基本假设

弦振动模型（18世纪由达朗贝尔等人首先系统研究）：给定一根两端固定的拉紧的均匀柔软的弦，其长度为L，在外力作用下在平衡位置附近作微小的横振动，求在不同时刻弦线的形状。

理想化假设：

1. 弦是均匀的，弦的截面直径与弦的长度相比可以忽略，因此弦可以视为 一根曲线，它的线密度 $\boldsymbol{\rho}$ 是常数。
2. 弦在某一平面内做微小振动，即弦的位置始终在一直线段附近，而弦上各点均在同一平面内垂直于该直线的方向上作微小振动。
3. 弦是柔软的，它在形变时不抵抗弯曲，弦上各质点间的张力方向与弦的切线方向一致，且弦的伸长形变与张力的关系服从Hooke定律（即弦在各点的伸长形变与该点的张力成正比）。

冲量：冲量是力对时间的积累效应，即力对时间的积分。

动量：物体的质量和速度的乘积。

牛顿第二定律： 作用在物体上的力 $\boldsymbol{=}$ 物体的质量 $\boldsymbol{\times}$ 物体的加速度

动量守恒定律： 外力产生的冲量（$t_1 \leq t \leq t_2$） $\boldsymbol{=}$ 动量的变化（$t_2$时刻动量$-t_1$时刻动量）

弦振动方程的导出

取弦的平衡位置为 $x$ 轴，在弦线运动的平面内，垂直于弦线平衡位置且通过弦线一个端点的直线为 $u$ 轴。任意时刻 $t$，弦线上各点的位移可表示为：$u = u(x, t)$

弦振动示意图

在弦上任意截取一段区间 $[x_1, x_2]$，考虑其在时段 $[t_1, t_2]$ 内的动量变化：

• 设 $\rho$ 为弦的线密度，
• $f_0$ 为作用在弦线上、垂直于平衡位置的强迫外力密度（单位长度的外力）。

则任意时刻 $t$，线段 $[x_1, x_2]$ 的动量为：

$$\int_{x_1}^{x_2} \rho \frac{\partial u}{\partial t} \, dx$$

时段 $[t_1, t_2]$ 内，线段 $[x_1, x_2]$ 的动量变化为末动量减初动量，即：

$$\int_{x_1}^{x_2} \left( \rho \frac{\partial u}{\partial t} \right)_{t=t_2} dx - \int_{x_1}^{x_2} \left( \rho \frac{\partial u}{\partial t} \right)_{t=t_1} dx$$

弦段 $[x_1, x_2]$ 受到两类力：

1. 外力 $f_0$；
2. 周围弦线通过端点作用于弦段 $[x_1, x_2]$ 的张力。

$f_0$的冲量

时段 $[t_1, t_2]$ 内，外力 $f_0$ 对弦段 $[x_1, x_2]$ 的冲量为：

$$\int_{t_1}^{t_2} \int_{x_1}^{x_2} f_0 \, dx dt$$

周围线通过端点作用于弦段 $[x_1, x_2]$ 的张力

记

• 弦上 $x$ 点在时刻 $t$ 的张力为 $T(x, t)$
• $\alpha_1$：弦在 $x_1$ 处切线与 $x$ 轴正方向的夹角；
• $\alpha_2$：弦在 $x_2$ 处切线与 $x$ 轴正方向的夹角。

考虑弦段 $[x_1, x_2]$ 的弧长 $\Delta s$，其精确表达式为：

$$\Delta s = \int_{x_1}^{x_2} \sqrt{1 + \left( \frac{\partial u}{\partial x} \right)^2} \, dx$$

基于微小振动假设（$\dfrac{\partial u}{\partial x}$ 很小，其平方为高阶小量），弧长可近似为：

$$\Delta s \approx \int_{x_1}^{x_2} dx = x_2 - x_1 = \Delta x$$

可以认为弦段在振动中无伸长。结合Hooke定律：张力 $T(x, t)$ 与时间 $t$ 无关，即 $T(x, t) = T(x)$。

弦振动示意图

记张力 $\boldsymbol{T}(x)$ 的大小为 $T(x)$，分析其在 $x$（水平）和 $u$（垂直）方向的分力：

• 端点 $x_1$ 处，张力 $\boldsymbol{T}(x_1)$ 的分力：

  $$T(x_1)\cos\alpha_1 \quad (\text{水平分量}), \quad T(x_1)\sin\alpha_1 \quad (\text{垂直分量})$$

• 端点 $x_2$ 处，张力 $\boldsymbol{T}(x_2)$ 的分力：

  $$T(x_2)\cos\alpha_2 \quad (\text{水平分量}), \quad T(x_2)\sin\alpha_2 \quad (\text{垂直分量})$$

弦仅做垂直于 $x$ 轴的横向振动，故水平方向合力必为零：

$$T(x_1)\cos\alpha_1 + T(x_2)\cos\alpha_2 = 0$$

结合微小振动假设，近似有：

$$\cos\alpha_1 \approx -1, \quad \cos\alpha_2 \approx 1$$

代入水平合力方程，得 张力为常数：

$$T(x_1) = T(x_2) = T_0$$

由于 $\pi - \alpha_1, \alpha_2$ 都很小，可认为：

• $x_1$ 处：$\sin\alpha_1 = \sin(\pi - \alpha_1) \approx \tan(\pi - \alpha_1) = \left. \dfrac{\partial u(x,t)}{\partial x} \right|_{x=x_1}$
• $x_2$ 处：$\sin\alpha_2 \approx \tan\alpha_2 = \left. \dfrac{\partial u(x,t)}{\partial x} \right|_{x=x_2}$

张力在垂直方向（$u$ 方向）的合力为：

$$T_0 \sin\alpha_2 - T_0 \sin\alpha_1 = T_0 \left( \left. \dfrac{\partial u(x,t)}{\partial x} \right|_{x=x_2} - \left. \dfrac{\partial u(x,t)}{\partial x} \right|_{x=x_1} \right)$$

垂直合力对时间的积分（冲量）为：

$$\int_{t_1}^{t_2} T_0 \left( \left. \dfrac{\partial u(x,t)}{\partial x} \right|_{x=x_2} - \left. \dfrac{\partial u(x,t)}{\partial x} \right|_{x=x_1} \right) dt$$

由动量守恒定律，

$$\int_{t_1}^{t_2} \int_{x_1}^{x_2} f_0 \, dx dt + \int_{t_1}^{t_2} T_0 \left( \left. \frac{\partial u(x,t)}{\partial x} \right|_{x=x_2} - \left. \frac{\partial u(x,t)}{\partial x} \right|_{x=x_1} \right) dt = \int_{x_1}^{x_2} \left( \rho \frac{\partial u}{\partial t} \right)_{t=t_2} dx - \int_{x_1}^{x_2} \left( \rho \frac{\partial u}{\partial t} \right)_{t=t_1} dx$$

移项，将差项展开为积分形式（此处假设函数性质足够好），

$$\int_{t_1}^{t_2} dt \int_{x_1}^{x_2} f_0 dx = \int_{x_1}^{x_2} \left[ \int_{t_1}^{t_2} \frac{\partial}{\partial t} \left( \rho \frac{\partial u}{\partial t} \right) dt \right] dx - \int_{t_1}^{t_2} T_0 \left[ \int_{x_1}^{x_2} \frac{\partial}{\partial x} \left( \frac{\partial u}{\partial x} \right)dx \right] dt$$

交换积分次序，合并之（此处假设函数性质足够好），

$$\int_{t_1}^{t_2} dt \int_{x_1}^{x_2} f_0 dx = \int_{t_1}^{t_2} dt \int_{x_1}^{x_2} \left[ \frac{\partial}{\partial t} \left( \rho \frac{\partial u}{\partial t} \right) - \frac{\partial}{\partial x} \left( T_0 \frac{\partial u}{\partial x} \right) \right] dx$$

由于区间 $[x_1, x_2]$ 和 $[t_1, t_2]$ 是任意选取的，被积函数必须恒等，因此得到弦振动方程：

$$\frac{\partial}{\partial t} \left( \rho \frac{\partial u}{\partial t} \right) - \frac{\partial}{\partial x} \left( T_0 \frac{\partial u}{\partial x} \right) = f_0 \quad (0 < x < L,\, t > 0)$$

若弦是均匀的（线密度 $\rho$ 为常数），则方程可简化为非齐次弦振动方程：

$$\frac{\partial^2 u}{\partial t^2} - a^2 \frac{\partial^2 u}{\partial x^2} = f \quad (0 < x < L,\, t > 0)$$

其中，

• 波速平方：$a^2 = \dfrac{T_0}{\rho}$，$a$ 是弦的波速
• 等效外力密度：$f(x, t) = \dfrac{f_0(x, t)}{\rho}$，

经典解：若函数 $u(x, t)$ 具有方程所需的各阶连续偏导数，且代入后使方程恒成立，则称 $u(x, t)$ 为该方程的 经典解。

方程描述了弦的位移 $u(x, t)$ 满足的一般性运动规律，但仅靠方程无法唯一确定弦的运动——还需结合 初始条件（初始位移、初始速度）和 边界条件（端点约束）。

定解条件与定解问题

初始条件

弦的运动需结合 初始状态（初始位移、初始速度）：

• 初始位移：$t=0$ 时，弦上各点的位移分布。

  $$u(x, 0) = \varphi(x)$$

• 初始速度：$t=0$ 时，弦上各点的速度分布，$u_t$ 表示 $\dfrac{\partial u}{\partial t}$。

  $$u_t(x, 0) = \psi(x)$$

Dirichlet边界条件（第一类边界条件）

已知端点的 位移变化，数学形式为：

$$u(0, t) = g_1(t), \quad u(\ell, t) = g_2(t) \quad (t \geq 0)$$

• 特殊情况：当 $g_1(t) = g_2(t) = 0$ 时，称弦线具有固定端。

Neumann边界条件（第二类边界条件）

已知端点所受 垂直方向的外力，数学形式为：

$$-\left. T \frac{\partial u}{\partial x} \right|_{x=0} = g_1(t), \quad \left. T \frac{\partial u}{\partial x} \right|_{x=\ell} = g_2(t) \quad (t \geq 0)$$

• 特殊情况：当 $g_1(t) = g_2(t) = 0$ 时，称弦线具有自由端。

Robin边界条件（第三类边界条件）

一般形式为：

$$-\left. T \frac{\partial u}{\partial x} \right|_{x=0} + \alpha_1 u(0, t) = g_1(t), \quad \left. T \frac{\partial u}{\partial x} \right|_{x=\ell} + \alpha_2 u(\ell, t) = g_2(t) \quad (t \geq 0)$$

其中 $\alpha_1, \alpha_2 > 0$。

定解问题

定解问题：由 偏微分方程 与 定解条件（初始条件 + 边界条件）共同构成，用于唯一确定物理过程的解。

• 混合问题：$\boldsymbol{\text{偏微分方程} + \text{初始条件} + \text{边界条件}}$
• 初值（Cauchy）问题：$\boldsymbol{\text{偏微分方程} + \text{初始条件}}$，考虑无限区域：$\displaystyle -\infty < x < \infty,\ t \geq 0$

波动方程的推广

弦振动方程的适用范围远不止弦的横向振动，还可描述杆的纵振动（位移沿杆长方向）、声波传播、电磁波传播等；因此，弦振动方程通常被称为 一维波动方程（“一维”指空间维度，时间为另一维度）。

对于 $n$ 维空间（如 $n=2$ 对应平面波，$n=3$ 对应空间波），波动方程推广为：

$$\frac{\partial^2 u}{\partial t^2} - a^2 \Delta u = f$$

其中：

• $\Delta u$ 是 Laplace算子，定义为 $\Delta u = \sum_{i=1}^n \frac{\partial^2 u}{\partial x_i^2}$；
• $n$ 为维数
• $a$ 为波速（常数），$f$ 为外力密度（非齐次项）。

高维波动方程的定解条件

初值条件： 对 $n$ 维空间中的有界开区域 $\Omega \subset \mathbb{R}^n$，初始时刻（$t=0$）的状态由以下条件描述：

• 初始位移：

  $$u(\boldsymbol{x}, 0) = \varphi(x_1, \dots, x_n) ,\quad \boldsymbol{x} = (x_1, \dots, x_n) \in \Omega$$

• 初始速度：

  $$u_t(\boldsymbol{x}, 0) = \psi(x_1, \dots, x_n) ,\quad \boldsymbol{x} = (x_1, \dots, x_n) \in \Omega$$

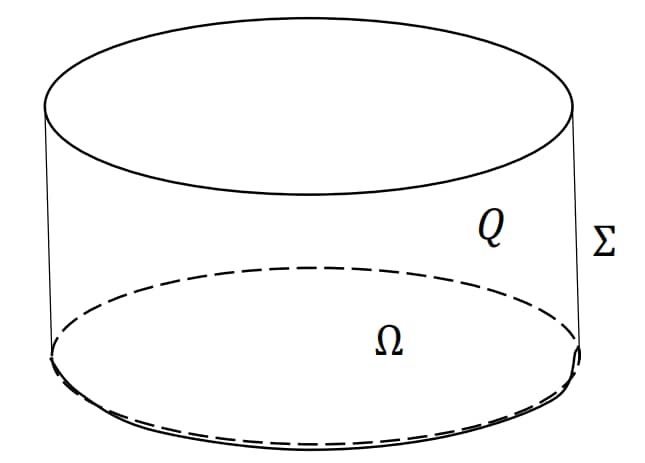n维波动方程示意图

边值条件：
$\Omega \subset \mathbb{R}^n$ 是有界开区域，

• $Q = \Omega \times [0, \infty)$：空间区域 $\Omega$ 与时间区间 $[0, \infty)$ 的笛卡尔积（柱形时空域），
• $\Sigma = \partial\Omega \times (0, \infty)$：$\Omega$ 的边界 $\partial\Omega$ 与时间区间 $(0, \infty)$ 的笛卡尔积（柱形边界，不含初始时刻 $t=0$）。

第一边界条件（Dirichlet 型）
直接约束边界 $\Sigma$ 上的 位移：

$$\left. u \right|_{\Sigma} = g(x_1, \dots, x_n, t)$$

第二边界条件（Neumann 型）
约束边界 $\Sigma$ 上的 法向导数（$\boldsymbol{n}$ 为 $\partial\Omega$ 的单位外法向量，$\dfrac{\partial u}{\partial \boldsymbol{n}}$ 表示 $u$ 沿 $\boldsymbol{n}$ 方向的偏导数）：

$$\left. \frac{\partial u}{\partial \boldsymbol{n}} \right|_{\Sigma} = g(x_1, \dots, x_n, t)$$

第三边界条件（Robin 型）
约束边界 $\Sigma$ 上 位移与法向导数的线性组合（$\alpha > 0$ 为常数，如弹性支撑的劲度系数）：

$$\left. \left( \frac{\partial u}{\partial \boldsymbol{n}} + \alpha u \right) \right|_{\Sigma} = g(x_1, \dots, x_n, t)$$

平衡态方程
当系统处于平衡态（时间二阶导数为零，即 $\dfrac{\partial^2 u}{\partial t^2} = 0$）时，波动方程退化为 平衡态方程（稳态方程）

$$-a^2 \Delta u = f(\boldsymbol{x})$$

其中 $\boldsymbol{x} = (x_1, \dots, x_n) \in \Omega \subset \mathbb{R}^n$，$\Delta$ 为 $n$ 维Laplace算子，$f(\boldsymbol{x})$ 是非齐次项。

边界条件
设空间边界为 $\Sigma = \partial\Omega$（因平衡态无时间变化，边界不含时间变量），三类边界条件形式如下：

第一边界条件（Dirichlet 型）

$$\left. u \right|_{\Sigma} = g(x_1, \dots, x_n)$$

第二边界条件（Neumann 型）

$$\left. \frac{\partial u}{\partial \boldsymbol{n}} \right|_{\Sigma} = g(x_1, \dots, x_n)$$

第三边界条件（Robin 型）

$$\left. \left( \frac{\partial u}{\partial \boldsymbol{n}} + \alpha u \right) \right|_{\Sigma} = g(x_1, \dots, x_n)$$